Logaritmi sa različitim bazama i istim eksponentima. Formule logaritama. Logaritmi su primjeri rješenja. Decimalni i prirodni logaritmi

Definicija logaritma

Logaritam broja b prema bazi a je eksponent na koji trebate podići a da biste dobili b.

Broj e u matematici je uobičajeno da se označava granica kojoj izraz teži

Broj e je iracionalan broj- broj neuporediv sa jedinicom, ne može se tačno izraziti ni kao celina ni kao razlomak racionalno broj.

Pismo e- prvo slovo latinske riječi exonere- razmetati se, otuda i naziv u matematici eksponencijalna- eksponencijalna funkcija.

Broj e naširoko koristi u matematici, iu svim naukama, na ovaj ili onaj način koristeći matematičke proračune za svoje potrebe.

Logaritmi. Svojstva logaritama

Definicija: logaritam pozitivan broj b u bazi je eksponent c na koji morate podići broj a da biste dobili broj b.

Osnovni logaritamski identitet:

7) Formula za prelazak na novu bazu:

lna = log e a, e ≈ 2,718…

Zadaci i testovi na temu „Logaritmi. Svojstva logaritama»

• Logaritmi - Važne teme za ponavljanje ispita iz matematike

Da biste uspješno obavili zadatke na ovu temu, morate znati definiciju logaritma, svojstva logaritma, osnovni logaritamski identitet, definicije decimalnog i prirodnog logaritma. Glavni tipovi zadataka na ovu temu su zadaci za izračunavanje i pretvaranje logaritamskih izraza. Razmotrimo njihovo rješenje na sljedećim primjerima.

Odluka: Koristeći svojstva logaritama, dobijamo

Odluka: koristeći svojstva stepena, dobijamo

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Svojstva logaritama, formulacije i dokazi.

Logaritmi imaju broj karakteristična svojstva. U ovom članku analizirat ćemo glavne svojstva logaritama. Ovdje dajemo njihove formulacije, zapisujemo svojstva logaritama u obliku formula, pokazujemo primjere njihove primjene, a također dajemo dokaze o svojstvima logaritama.

Navigacija po stranici.

Osnovna svojstva logaritama, formule

Radi lakšeg pamćenja i upotrebe, predstavljamo osnovna svojstva logaritama kao lista formula. U sljedećem dijelu dajemo njihove formulacije, dokaze, primjere upotrebe i potrebna objašnjenja.

Privatno svojstvo logaritma: , gdje je a>0, a≠1, x>0, y>0.

Posljedica: , gdje je a>0 , a≠1 , n – prirodni broj, veći od jedan, b>0 .

Korol 1: , a>0 , a≠1 , b>0 , b≠1 .

Korol 2: , a>0 , a≠1 , b>0 , p i q su realni brojevi, q≠0 , posebno za b=a imamo .

Izjave i dokazi imovine

Prelazimo na formulaciju i dokaz zapisanih svojstava logaritama. Sva svojstva logaritma dokazuju se na osnovu definicije logaritma i osnovnog logaritamskog identiteta koji iz njega proizlazi, kao i svojstava stepena.

Počnimo sa svojstva logaritma jedinice. Njegova formulacija je sljedeća: logaritam jedinice nula, to je, log a 1=0 za bilo koje a>0 , a≠1 . Dokaz je jednostavan: pošto je a 0 =1 za bilo koje a koje zadovoljava gornje uslove a>0 i a≠1, onda dokazana jednakost log a 1=0 odmah slijedi iz definicije logaritma.

Navedimo primjere primjene razmatranog svojstva: log 3 1=0 , lg1=0 i .

Pređimo na sljedeću imovinu: logaritam broja jednakog bazi, jednako jedan , to je, log a a=1 za a>0 , a≠1 . Zaista, pošto je a 1 =a za bilo koje a , onda je po definiciji logaritma log a a=1 .

Primjeri korištenja ovog svojstva logaritama su log 5 5=1 , log 5.6 5.6 i lne=1 .

Logaritam stepena broja jednakog osnovici logaritma jednak je eksponentu. Ovo svojstvo logaritma odgovara formuli oblika log a a p =p, gdje je a>0, a≠1 i p bilo koji realan broj. Ovo svojstvo direktno slijedi iz definicije logaritma. Imajte na umu da vam omogućava da odmah odredite vrijednost logaritma, ako je moguće predstaviti broj pod znakom logaritma kao stupanj baze, o tome ćemo više govoriti u članku o izračunavanju logaritma.

Na primjer, log 2 2 7 =7 , log10 -4 =-4 i .

Logaritam proizvoda dva pozitivna broja x i y jednak je proizvodu logaritama ovih brojeva: log a (x y)=log a x+log a y, a>0 , a≠1 . Dokažimo svojstvo logaritma proizvoda. Zbog svojstava stepena a log a x + log a y =a log a x a log a y , a pošto je po glavnom logaritamskom identitetu log a x =x i log a y =y , onda je log a x a log a y =x y . Dakle, log a x+log a y =x y , odakle tražena jednakost slijedi iz definicije logaritma.

Pokažimo primjere korištenja svojstva logaritma proizvoda: log 5 (2 3)=log 5 2+log 5 3 i .

Svojstvo logaritma proizvoda može se generalizirati na proizvod konačnog broja n pozitivnih brojeva x 1 , x 2 , …, x n kao log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Ova se jednakost lako može dokazati metodom matematičke indukcije.

Na primjer, prirodni logaritam proizvoda može se zamijeniti zbirom tri prirodna logaritma brojeva 4 , e i .

Logaritam količnika dva pozitivna broja x i y jednaka je razlici između logaritama ovih brojeva. Svojstvo kvocijentnog logaritma odgovara formuli oblika , gdje su a>0, a≠1, x i y neki pozitivni brojevi. Valjanost ove formule dokazuje se kao i formula za logaritam proizvoda: pošto , zatim po definiciji logaritma .

Evo primjera korištenja ovog svojstva logaritma: .

Idemo dalje svojstvo logaritma stepena. Logaritam stepena jednak je proizvodu eksponenta i logaritma modula baze ovog stepena. Ovo svojstvo logaritma stepena zapisujemo u obliku formule: log a b p =p log a |b|, gdje su a>0, a≠1, b i p brojevi takvi da stepen b p ima smisla i b p >0.

Prvo ćemo dokazati ovo svojstvo za pozitivno b . Osnovni logaritamski identitet nam omogućava da broj b predstavimo kao log a b, zatim b p =(a log a b) p, a rezultirajući izraz, zbog svojstva snage, jednak je a p log a b. Tako dolazimo do jednakosti b p =a p log a b , iz koje, po definiciji logaritma, zaključujemo da je log a b p =p log a b .

Ostaje dokazati ovo svojstvo za negativan b . Ovdje napominjemo da izraz log a b p za negativan b ima smisla samo za parne eksponente p (pošto vrijednost stepena b p mora biti veća od nule, inače logaritam neće imati smisla), a u ovom slučaju b p =|b| p . Tada je b p =|b| p =(a log a |b|) p =a p log a |b| , odakle log a b p =p log a |b| .

Na primjer, i ln(-3) 4 =4 ln|-3|=4 ln3 .

To proizilazi iz prethodnog svojstva svojstvo logaritma iz korijena: logaritam korijena n-tog stepena jednak je umnošku razlomka 1/n i logaritma korijenskog izraza, odnosno gdje je a>0, a≠1, n prirodni broj veći od jedan, b>0.

Dokaz se zasniva na jednakosti (pogledajte definiciju eksponenta sa razlomačnim eksponentom), koja vrijedi za bilo koji pozitivan b , i svojstvu logaritma stepena: .

Evo primjera korištenja ovog svojstva: .

Sada dokažimo formulu konverzije u novu bazu logaritma vrsta . Da biste to učinili, dovoljno je dokazati valjanost jednakosti log c b=log a b log c a . Osnovni logaritamski identitet nam omogućava da broj b predstavimo kao log a b, zatim log c b=log c a log a b. Ostaje koristiti svojstvo logaritma stepena: log c a log a b = log a b log c a . Time je dokazana jednakost log c b=log a b log c a, što znači da je dokazana i formula za prelazak na novu bazu logaritma .

Pokažimo nekoliko primjera primjene ovog svojstva logaritama: i .

Formula za prelazak na novu bazu omogućava vam da pređete na rad sa logaritmima koji imaju „prikladnu“ bazu. Na primjer, može se koristiti za prebacivanje na prirodne ili decimalne logaritme tako da možete izračunati vrijednost logaritma iz tablice logaritama. Formula za prijelaz na novu bazu logaritma također omogućava u nekim slučajevima da se pronađe vrijednost datog logaritma, kada su poznate vrijednosti nekih logaritama s drugim bazama.

Često se koristi poseban slučaj formule tranzicije na novu bazu logaritma za c=b oblika. Ovo pokazuje da su log a b i log b a međusobno inverzni brojevi. Na primjer, .

Često se koristi i formula, što je zgodno za pronalaženje vrijednosti logaritma. Da bismo potvrdili naše riječi, pokazat ćemo kako se pomoću njega izračunava vrijednost logaritma obrasca. Imamo . Da bismo dokazali formulu, dovoljno je koristiti formulu prijelaza na novu bazu logaritma a: .

Ostaje dokazati svojstva poređenja logaritama.

Koristimo suprotnu metodu. Pretpostavimo da je za a 1 >1, a 2 >1 i a 1 2 i za 0 1 log a 1 b≤log a 2 b tačno. Po svojstvima logaritama, ove nejednačine se mogu prepisati kao i respektivno, a iz njih proizilazi da je log b a 1 ≤log b a 2 i log b a 1 ≥log b a 2, respektivno. Zatim po svojstvima snaga sa istih osnova moraju biti zadovoljene jednakosti b log b a 1 ≥b log b a 2 i b log b a 1 ≥b log b a 2, odnosno a 1 ≥a 2 . Dakle, došli smo do kontradikcije sa uslovom a 1 2 . Ovim je dokaz završen.

Osnovna svojstva logaritama

• Materijali za lekciju
• Preuzmite sve formule

Logaritmi, kao i svaki broj, mogu se sabirati, oduzimati i pretvarati na sve moguće načine. Ali pošto logaritmi nisu sasvim obični brojevi, ovdje postoje pravila koja se nazivaju osnovna svojstva.

Ova pravila se moraju znati - bez njih se ne rješava nijedan ozbiljan problem. logaritamski problem. Osim toga, vrlo ih je malo - sve se može naučiti u jednom danu. Pa počnimo.

Sabiranje i oduzimanje logaritama

Razmotrimo dva logaritma sa istom bazom: log a x i log a y. Tada se mogu sabirati i oduzimati i:

Dakle, zbir logaritama je jednak logaritmu proizvoda, a razlika je logaritam količnika. Bilješka: ključni trenutak ovdje - iste osnove. Ako su osnove različite, ova pravila ne funkcionišu!

Ove formule će vam pomoći da izračunate logaritamski izrazčak i kada se njegovi pojedinačni dijelovi ne uzimaju u obzir (vidi lekciju "Šta je logaritam"). Pogledajte primjere - i pogledajte:

Zadatak. Pronađite vrijednost izraza: log 6 4 + log 6 9.

Pošto su baze logaritama iste, koristimo formulu sume:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadatak. Pronađite vrijednost izraza: log 2 48 − log 2 3.

Osnove su iste, koristimo formulu razlike:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadatak. Pronađite vrijednost izraza: log 3 135 − log 3 5.

Opet, baze su iste, tako da imamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kao što vidite, originalni izrazi su sastavljeni od "loših" logaritama, koji se ne razmatraju zasebno. Ali nakon transformacija ispadaju sasvim normalni brojevi. Na osnovu ove činjenice, mnogi test papiri. Da, ta kontrola - slični izrazi u punoj ozbiljnosti (ponekad - bez izmjena) se nude na ispitu.

Uklanjanje eksponenta iz logaritma

Sada da malo zakomplikujemo zadatak. Šta ako postoji stepen u bazi ili argumentu logaritma? Tada se eksponent ovog stepena može izvaditi iz predznaka logaritma prema sljedećim pravilima:

• log a x n = n log a x ;
• 
• 

Lako je to vidjeti poslednje pravilo prati prva dva. Ali ipak je bolje zapamtiti to - u nekim slučajevima to će značajno smanjiti količinu proračuna.

Naravno, sva ova pravila imaju smisla ako se poštuje ODZ logaritam: a > 0, a ≠ 1, x > 0. I još nešto: naučite primjenjivati ​​sve formule ne samo s lijeva na desno, već i obrnuto, tj. možete unijeti brojeve ispred znaka logaritma u sam logaritam. To je ono što se najčešće traži.

Zadatak. Pronađite vrijednost izraza: log 7 49 6 .

Oslobodimo se stepena u argumentu prema prvoj formuli:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadatak. Pronađite vrijednost izraza:

[Natpis slike]

Imajte na umu da je imenilac logaritam čija su osnova i argument tačni potenci: 16 = 2 4 ; 49 = 72. Imamo:

[Natpis slike]

Mislim da posljednji primjer treba pojasniti. Gdje su nestali logaritmi? Do poslednjeg trenutka radimo samo sa imeniocem. Osnovu i argument logaritma koji tu stoji predstavili su u obliku stepeni i izvadili indikatore - dobili su razlomak od tri sprata.

Pogledajmo sada glavni razlomak. Brojilac i imenilac imaju isti broj: log 2 7. Pošto je log 2 7 ≠ 0, možemo smanjiti razlomak - 2/4 će ostati u nazivniku. Prema pravilima aritmetike, četvorka se može prenijeti u brojilac, što je i učinjeno. Rezultat je odgovor: 2.

Prelazak na novu osnovu

Govoreći o pravilima za sabiranje i oduzimanje logaritama, posebno sam naglasio da oni rade samo sa istim osnovama. Šta ako su baze različite? Šta ako nisu tačne snage istog broja?

Formule za prelazak na novu bazu dolaze u pomoć. Formuliramo ih u obliku teoreme:

Neka je dat logaritam log a x. Tada je za bilo koji broj c takav da je c > 0 i c ≠ 1 tačna jednakost:

[Natpis slike]

Konkretno, ako stavimo c = x , dobićemo:

[Natpis slike]

Iz druge formule proizilazi da je moguće zamijeniti bazu i argument logaritma, ali se u ovom slučaju cijeli izraz „obrće“, tj. logaritam je u nazivniku.

Ove formule se rijetko nalaze u običnim numeričke izraze. Koliko su zgodne moguće je procijeniti tek prilikom odlučivanja logaritamske jednačine i nejednakosti.

Međutim, postoje zadaci koji se nikako ne mogu riješiti osim prelaskom na novu osnovu. Razmotrimo nekoliko od ovih:

Zadatak. Pronađite vrijednost izraza: log 5 16 log 2 25.

Imajte na umu da su argumenti oba logaritma tačni eksponenti. Izvadimo indikatore: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Sada okrenimo drugi logaritam:

[Natpis slike]

Budući da se proizvod ne mijenja permutacijom faktora, mirno smo pomnožili četiri i dva, a zatim izračunali logaritme.

Zadatak. Pronađite vrijednost izraza: log 9 100 lg 3.

Osnova i argument prvog logaritma su tačni potenci. Hajde da to zapišemo i riješimo se indikatora:

[Natpis slike]

Sada se riješimo decimalnog logaritma pomicanjem na novu bazu:

[Natpis slike]

Osnovni logaritamski identitet

Često je u procesu rješavanja potrebno prikazati broj kao logaritam na datu bazu. U ovom slučaju, formule će nam pomoći:

1. n = log a a n

2. U prvom slučaju, broj n postaje eksponent u argumentu. Broj n može biti apsolutno bilo koji, jer je to samo vrijednost logaritma.

   Druga formula je zapravo parafrazirana definicija. To se zove osnovni logaritamski identitet.

   Zaista, šta će se dogoditi ako se broj b podigne na takav stepen da broj b na ovaj stepen daje broj a? Tako je: ovo je isti broj a . Pažljivo pročitajte ovaj odlomak ponovo - mnogi ljudi ga "zakače".

   Kao i nove formule osnovne konverzije, osnovni logaritamski identitet je ponekad jedino moguće rješenje.

   [Natpis slike]

   Imajte na umu da je log 25 64 = log 5 8 - samo uzmite kvadrat baze i argument logaritma. S obzirom na pravila za množenje potencija sa istom osnovom, dobijamo:

   [Natpis slike]

   Ako neko nije upoznat, ovo je bio pravi zadatak sa Jedinstvenog državnog ispita 🙂

   Logaritamska jedinica i logaritamska nula

   U zaključku ću dati dva identiteta koja je teško nazvati svojstvima – radije, to su posljedice iz definicije logaritma. Stalno se nalaze u problemima i, iznenađujuće, stvaraju probleme čak i "naprednim" učenicima.

   1. log a a = 1 je logaritamska jedinica. Zapamtite jednom za svagda: logaritam bilo koje baze a iz same te baze jednak je jedan.
   2. log a 1 = 0 je logaritamska nula. Baza a može biti bilo koja, ali ako je argument jedan - logaritam je nula! Zato što je 0 = 1 direktna posljedica definicije.

   To je sva imovina. Obavezno vježbajte u njihovoj primjeni! Preuzmite cheat sheet na početku lekcije, odštampajte ga - i riješite probleme.

   Logaritam. Svojstva logaritma (sabiranje i oduzimanje).

   Svojstva logaritma proizilaze iz njegove definicije. I tako logaritam broja b razumom a definiran kao eksponent na koji se broj mora podići a da dobijem broj b(logaritam postoji samo za pozitivne brojeve).

   Iz ove formulacije proizilazi da je proračun x=log a b, je ekvivalentno rješavanju jednačine ax=b. Na primjer, log 2 8 = 3 jer 8 = 2 3 . Formulacija logaritma omogućava da se opravda ako b=a c, zatim logaritam broja b razumom a jednaki With. Takođe je jasno da je tema logaritma usko povezana sa temom stepena broja.

   Sa logaritmima, kao i sa svakim brojevima, možete izvesti operacije sabiranja, oduzimanja i transformisati na svaki mogući način. Ali s obzirom na činjenicu da logaritmi nisu sasvim obični brojevi, ovdje vrijede njihova posebna pravila, koja se nazivaju osnovna svojstva.

   Sabiranje i oduzimanje logaritama.

   Uzmite dva logaritma sa istom bazom: log x i log a y. Zatim uklonite moguće je izvršiti operacije sabiranja i oduzimanja:

   kao što vidimo, zbir logaritama jednako je logaritmu proizvoda, i razlika logaritmi- logaritam količnika. I to je istina ako su brojevi a, X i at pozitivno i a ≠ 1.

   Važno je napomenuti da su glavni aspekt u ovim formulama iste baze. Ako se baze razlikuju jedna od druge, ova pravila ne vrijede!

   Pravila za sabiranje i oduzimanje logaritama sa istim osnovama čitaju se ne samo s lijeva na desno, već i obrnuto. Kao rezultat, imamo teoreme za logaritam proizvoda i logaritam kvocijenta.

   Logaritam proizvoda dva pozitivna broja jednak je zbiru njihove logaritme ; parafrazirajući ovu teoremu, dobijamo sljedeće, ako su brojevi a, x i at pozitivno i a ≠ 1, zatim:

   Logaritam količnika dva pozitivna broja jednaka je razlici između logaritama dividende i djelitelja. Drugim riječima, ako su brojevi a, X i at pozitivno i a ≠ 1, zatim:

   Za rješavanje primjenjujemo gornje teoreme primjeri:

   Ako brojevi x i at su onda negativni formula logaritma proizvoda postaje besmisleno. Dakle, zabranjeno je pisati:

   budući da izrazi log 2 (-8) i log 2 (-4) uopće nisu definirani (logaritamska funkcija at= dnevnik 2 X definirano samo za pozitivne vrijednosti argumenta X).

   Teorema proizvoda primjenjiv je ne samo na dva, već i na neograničen broj faktora. To znači da za svaki prirodni k i bilo koje pozitivne brojeve x 1 , x 2 , . . . ,x n postoji identitet:

   Od teoreme kvocijentnog logaritma može se dobiti još jedno svojstvo logaritma. Dobro je poznat taj dnevnik a 1= 0, dakle,

   Dakle, postoji jednakost:

   Logaritmi dva međusobno recipročna broja po istoj osnovi će se razlikovati jedno od drugog samo u znaku. dakle:

   Logaritam. Svojstva logaritama

   Logaritam. Svojstva logaritama

   Razmotrite jednakost. Javite nam vrijednosti i želimo da pronađemo vrijednost .

   Odnosno, tražimo eksponent na koji treba da se nagnete da biste dobili .

   Neka varijabla može uzeti bilo koju realnu vrijednost, tada se na varijable nameću sljedeća ograničenja: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Ako znamo vrijednosti i , a suočeni smo sa zadatkom pronalaženja nepoznatog, tada se u tu svrhu uvodi matematička operacija koja se zove logaritam.

   Da pronađemo vrijednost koju uzimamo logaritam broja on temelj :

   Logaritam broja prema bazi je eksponent na koji trebate podići da biste dobili .

   To je osnovni logaritamski identitet:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   je u suštini matematička notacija logaritamske definicije.

   Logaritam matematičke operacije je inverzna eksponencijalnost, dakle svojstva logaritama su usko povezani sa svojstvima stepena.

   Navodimo glavne svojstva logaritama:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Sljedeća grupa svojstava vam omogućava da eksponent izraza predstavite pod znakom logaritma ili koji stoji na bazi logaritma kao koeficijent prije znaka logaritma:

   6.

   7.

   8.

   9.

   Sledeća grupa formula omogućava vam da pređete od logaritma sa datom bazom na logaritam sa proizvoljnom bazom, i naziva se prelazne formule na novu bazu:

   10.

   12. (posledica iz svojstva 11)

   

   Sljedeća tri svojstva nisu dobro poznata, ali se često koriste pri rješavanju logaritamskih jednadžbi ili pri pojednostavljivanju izraza koji sadrže logaritme:

   13.

   14.

   15.

   Posebni slučajevi:

   — decimalni logaritam

   — prirodni logaritam

   Prilikom pojednostavljivanja izraza koji sadrže logaritme, primjenjuje se opći pristup:

   1. Upoznavanje decimale u obliku običnog.

   2. mešoviti brojevi predstavljeni kao nepravilni razlomci.

   3. Brojevi u osnovi logaritma i pod znakom logaritma razlažu se na proste faktore.

   4. Trudimo se da sve logaritme dovedemo na istu bazu.

   5. Primijeniti svojstva logaritama.

   Pogledajmo primjere pojednostavljivanja izraza koji sadrže logaritme.

   Primjer 1

   Izračunati:

   Pojednostavimo sve eksponente: naš zadatak je da ih dovedemo do logaritma čija je baza isti broj kao i baza eksponenta.

   ==(prema svojstvu 7)=(po svojstvu 6) =

   Zamijenite indikatore koje smo dobili u originalni izraz. Dobijamo:

   Odgovor: 5.25

   Primjer 2 Izračunajte:

   

   Sve logaritme dovodimo na bazu 6 (u ovom slučaju, logaritmi iz nazivnika razlomka će se „preseliti“ u brojilac):

   Razložimo brojeve pod znakom logaritma na proste faktore:

   Primijenite svojstva 4 i 6:

   Predstavljamo zamjenu

   Dobijamo:

   Odgovor: 1

   Logaritam . Osnovni logaritamski identitet.

   Svojstva logaritama. Decimalni logaritam. prirodni logaritam.

   logaritam pozitivan broj N u bazi (b > 0, b 1) naziva se eksponent x na koji treba podići b da biste dobili N .

   Ovaj unos je ekvivalentan sljedećem: b x = N .

   PRIMJERI: log 3 81 = 4 jer je 3 4 = 81 ;

   log 1/3 27 = – 3 jer (1/3) - 3 = 3 3 = 27 .

   Gornja definicija logaritma može se napisati kao identitet:

   

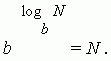
   Osnovna svojstva logaritama.

   2) log 1 = 0 jer b 0 = 1 .

   3) Logaritam proizvoda jednak je zbroju logaritama faktora:

   4) Logaritam kvocijenta jednak je razlici između logaritama dividende i djelitelja:

   5) Logaritam stepena jednak je umnošku eksponenta i logaritma njegove baze:

   Posljedica ovog svojstva je sljedeća: log root jednak je logaritmu korijenskog broja podijeljenog sa potencijom korijena:

   

   6) Ako je osnova logaritma stepen, onda je vrijednost recipročan stepena, može se izvaditi iz znaka log rime:

   

   Posljednja dva svojstva mogu se kombinirati u jednu:

   

   7) Formula za prijelazni modul (tj. prijelaz s jedne baze logaritma na drugu bazu):

   

   U konkretnom slučaju, kada N = a imamo:

   

   Decimalni logaritam pozvao osnovni logaritam 10. Označava se lg, tj. dnevnik 10 N= log N. Logaritmi brojeva 10, 100, 1000, . p su 1, 2, 3, …, redom, tj. imaju toliko pozitivnih

   jedinica, koliko je nula u logaritmskom broju nakon jedan. Logaritmi brojeva 0,1, 0,01, 0,001, . p su –1, –2, –3, …, respektivno, tj. imaju onoliko negativnih koliko ima nula u logaritmskom broju prije jedinice (uključujući nula cijelih brojeva). Logaritmi preostalih brojeva imaju razlomak koji se zove mantissa. Poziva se cijeli broj logaritma karakteristika. Za praktične primjene decimalni logaritmi su najpogodniji.

   prirodni logaritam pozvao osnovni logaritam e. Označava se sa ln, tj. log e N=ln N. Broj e je iracionalan, njegova približna vrijednost je 2,718281828. To je granica prema kojoj se broj (1 + 1 / n) n uz neograničeno povećanje n(cm. prva divna granica na stranici Ograničenja redoslijeda brojeva).
   Koliko god čudno izgledalo, prirodni logaritmi pokazalo se vrlo zgodnim za izvođenje raznih operacija vezanih za analizu funkcija. Izračunavanje baznih logaritama e mnogo brže od bilo koje druge osnove.

• Šta vam je danas potrebno da usvojite dijete u Rusiji? Usvajanje u Rusiji, pored odgovorne lične odluke, uključuje i niz procedura državne verifikacije kandidata. Čvrsta selekcija u pripremnoj fazi doprinosi više […]
• Besplatne informacije o TIN-u ili OGRN-u iz poreskog registra širom Rusije - na mreži Na Jedinstvenom portalu poreskih usluga, informacije o državna registracija pravna lica, individualni preduzetnici, […]
• Kazna za vožnju bez dokumenata (vozačka dozvola, osiguranje, STS) Ponekad, zbog zaborava, vozači sjednu za volan bez dozvole i dobiju kaznu za vožnju bez dokumenata. Podsjetimo da se vozač bez greške vozi s njim […]
• Cveće za muškarce. Kakvo cveće možete pokloniti muškarcu? Koje cveće se može pokloniti muškarcu? Nema toliko "muških" cvijeća, ali ima onih koje se poklanjaju muškarcima. Mala lista cvijeća pred vama: krizanteme. Roses. Karanfili. […]
• Memorandum je poseban oblik dokumenta koji se koristi u internom okruženju preduzeća i služi za brzo rješavanje tekućih proizvodnih problema. Obično se ovaj dokument sastavlja u svrhu izrade nekih […]
• Kada i kako dobiti fondovski dio penzije u Sberbanci? Sberbank je partnerska banka državnog penzionog fonda. Na osnovu toga, građani koji su izdali fondovsku penziju mogli bi prenijeti fondovsku […]
• Dječiji dodaci u Uljanovsku i region Uljanovsk u 2018. Osim toga, svi regioni imaju programe odobrene saveznim zakonom. Da vidimo na koga i na koje beneficije može da računa. Kao regionalne vlasti […]
• Detaljan vodič kako sastaviti punomoćje pojedinac na sudu U građanskoj ili arbitražnoj tužbi, u upravnom ili krivičnom predmetu, interese i tužioca i tuženog može zastupati advokat: […]

Date su glavne osobine prirodnog logaritma, graf, oblast definicije, skup vrijednosti, osnovne formule, izvod, integral, proširenje u niz stepena i reprezentacija funkcije ln x pomoću kompleksnih brojeva.

Definicija

prirodni logaritam je funkcija y = ln x, obrnuto od izlagač, x = e y , i bitak logaritam na osnovu broja e: ln x = log e x.

Prirodni logaritam se široko koristi u matematici jer njegov izvod ima najjednostavniji oblik: (ln x)′ = 1/ x.

Na osnovu definicije, baza prirodnog logaritma je broj e:
e ≅ 2.718281828459045...;
.

Grafikon funkcije y = ln x.

Grafikon prirodnog logaritma (funkcije y = ln x) se dobija iz eksponentna grafika zrcalni odraz oko prave linije y = x .

Prirodni logaritam je definiran na pozitivne vrijednosti varijabla x . Ona se monotono povećava u svom domenu definicije.

Kao x → 0 granica prirodnog logaritma je minus beskonačnost ( - ∞ ).

Kako je x → + ∞, granica prirodnog logaritma je plus beskonačnost ( + ∞). Za veliki x, logaritam raste prilično sporo. Bilo koji funkcija snage x a sa pozitivnim eksponentom a raste brže od logaritma.

Svojstva prirodnog logaritma

Domen definicije, skup vrijednosti, ekstremi, povećanje, smanjenje

Prirodni logaritam je monotono rastuća funkcija, tako da nema ekstrema. Glavna svojstva prirodnog logaritma prikazana su u tabeli.

ln x vrijednosti

log 1 = 0

Osnovne formule za prirodne logaritme

Formule koje proizlaze iz definicije inverzne funkcije:

Glavno svojstvo logaritma i njegove posljedice

Formula zamjene baze

Bilo koji logaritam se može izraziti prirodnim logaritmima koristeći formulu promjene baze:

Dokazi ovih formula su predstavljeni u odjeljku "logaritam".

Inverzna funkcija

Recipročna vrijednost za prirodni logaritam je izlagač.

Ako onda

Ako onda .

Derivat ln x

Derivat prirodnog logaritma:
.
Derivat prirodnog logaritma modula x:
.
Derivat n-tog reda:
.
Derivacija formula > > >

Integral

Izračunava se integral integracija po dijelovima :
.
dakle,

Izrazi u terminima kompleksnih brojeva

Razmotrimo funkciju kompleksne varijable z:
.
Izrazimo kompleksnu varijablu z preko modula r i argument φ :
.
Koristeći svojstva logaritma, imamo:
.
Or
.
Argument φ nije jednoznačno definiran. Ako stavimo
, gdje je n cijeli broj,
tada će to biti isti broj za različite n.

Dakle, prirodni logaritam, kao funkcija kompleksne varijable, nije jednoznačna funkcija.

Proširenje serije snaga

Za , proširenje se odvija:

Reference:
I.N. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokoškolskih ustanova, Lan, 2009.

Logaritam broja N razumom a naziva se eksponent X , na koju trebate podići a da dobijem broj N

Pod uslovom da
,
,

Iz definicije logaritma slijedi da
, tj.
- ova jednakost je osnovni logaritamski identitet.

Logaritmi na osnovu 10 nazivaju se decimalni logaritmi. Umjesto
pisati
.

osnovni logaritmi e nazivaju se prirodnim i označenim
.

Osnovna svojstva logaritama.

Logaritam jedinice za bilo koju bazu je nula

Logaritam proizvoda jednak je zbiru logaritama faktora.

3) Logaritam količnika je jednak razlici logaritama

Faktor
naziva se modulom prijelaza iz logaritma na bazi a na logaritme u osnovi b .

Koristeći svojstva 2-5, često je moguće svesti logaritam složenog izraza na rezultat jednostavnih aritmetičkih operacija nad logaritmima.

Na primjer,

Takve transformacije logaritma se nazivaju logaritmi. Transformacije recipročne od logaritama nazivaju se potenciranje.

Poglavlje 2. Elementi više matematike.

1. Ograničenja

ograničenje funkcije
je konačan broj A ako, kada težimo xx 0 za svako unapred određeno
, postoji broj
da čim
, onda
.

Funkcija koja ima ograničenje razlikuje se od nje za beskonačno mali iznos:
, gdje je - b.m.w., tj.
.

Primjer. Razmotrite funkciju
.

Kada težite
, funkcija y ide na nulu:

1.1. Osnovne teoreme o granicama.

Granica konstantne vrijednosti jednaka je ovoj konstantnoj vrijednosti

.

Granica zbira (razlike) konačnog broja funkcija jednaka je zbiru (razlici) granica ovih funkcija.

Granica proizvoda konačnog broja funkcija jednaka je proizvodu granica tih funkcija.

Granica kvocijenta dvije funkcije jednaka je količniku granica ovih funkcija ako granica nazivnika nije jednaka nuli.

Izvanredne granice

,
, gdje

1.2. Primjeri izračuna ograničenja

Međutim, nisu sve granice izračunate tako lako. Češće se izračun granice svodi na otkrivanje nesigurnosti tipa: ili .

.

2. Derivat funkcije

Neka imamo funkciju
, kontinuirano na segmentu
.

Argument dobio malo pojačanja
. Tada će se funkcija povećati
.

Vrijednost argumenta odgovara vrijednosti funkcije
.

Vrijednost argumenta
odgovara vrijednosti funkcije .

Shodno tome, .

Nađimo granicu ove relacije na
. Ako ova granica postoji, onda se naziva derivacijom date funkcije.

Definicija 3derivacije date funkcije
argumentacijom naziva se granica omjera prirasta funkcije i priraštaja argumenta, kada inkrement argumenta proizvoljno teži nuli.

Izvod funkcije
može se označiti na sljedeći način:

; ; ; .

Definicija 4Poziva se operacija nalaženja derivacije funkcije diferencijaciju.

2.1. Mehaničko značenje izvedenice.

Razmotrimo pravolinijsko kretanje nekog krutog tijela ili materijalne tačke.

Neka u nekom trenutku pokretna tačka
bio na distanci sa početne pozicije
.

Nakon nekog vremena
odmakla se
. Stav =- prosječna brzina materijalna tačka
. Nađimo granicu ovog omjera, uzimajući to u obzir
.

Shodno tome, određivanje trenutne brzine materijalne tačke se svodi na pronalaženje derivacije putanje u odnosu na vrijeme.

2.2. geometrijska vrijednost derivat

Pretpostavimo da imamo grafički definiranu neku funkciju
.

Rice. 1. Geometrijsko značenje izvedenice

Ako
, zatim poenta
, će se kretati duž krive, približavajući se tački
.

Shodno tome
, tj. vrijednost izvoda s obzirom na vrijednost argumenta numerički jednak tangentu ugla koji formira tangenta u datoj tački sa pozitivnim smerom ose
.

2.3. Tabela osnovnih formula diferencijacije.

Funkcija napajanja

Eksponencijalna funkcija

logaritamska funkcija

trigonometrijska funkcija

Inverzna trigonometrijska funkcija

2.4. Pravila diferencijacije.

Derivat od

Derivat zbira (razlike) funkcija

Derivat proizvoda dviju funkcija

Derivat kvocijenta dvije funkcije

2.5. Derivat od složena funkcija.

Neka funkcija
tako da se može predstaviti kao

i
, gdje je varijabla onda je srednji argument

Derivat kompleksne funkcije jednak je proizvodu izvoda date funkcije u odnosu na međuargument na derivaciju srednjeg argumenta u odnosu na x.

Primjer1.

Primjer 2.

3. Funkcijski diferencijal.

Neka bude
, diferencibilan na nekom intervalu
pusti to at ova funkcija ima izvod

,

onda možeš pisati

(1),

gdje - beskonačno mala količina,

jer at

Množenje svih pojmova jednakosti (1) sa
imamo:

Gdje
- b.m.v. višeg reda.

Vrijednost
naziva se diferencijal funkcije
i označeno

.

3.1. Geometrijska vrijednost diferencijala.

Neka funkcija
.

Fig.2. Geometrijsko značenje diferencijala.

.

Očigledno, diferencijal funkcije
jednak je inkrementu ordinate tangente u datoj tački.

3.2. Derivati ​​i diferencijali različitih redova.

Ako tamo
, onda
naziva se prvim izvodom.

Izvod prvog izvoda naziva se izvod drugog reda i piše se
.

Derivat n-tog reda funkcije
naziva se derivat (n-1) reda i piše se:

.

Diferencijal diferencijala funkcije naziva se drugi diferencijal ili diferencijal drugog reda.

.

.

3.3 Rješavanje bioloških problema pomoću diferencijacije.

Zadatak1. Istraživanja su pokazala da je rast kolonije mikroorganizama u skladu sa zakonom
, gdje N – broj mikroorganizama (u hiljadama), t – vrijeme (dani).

b) Hoće li se populacija kolonije povećati ili smanjiti tokom ovog perioda?

Odgovori. Kolonija će rasti.

Zadatak 2. Voda u jezeru se periodično ispituje radi kontrole sadržaja patogenih bakterija. Kroz t dana nakon testiranja, koncentracija bakterija se određuje omjerom

.

Kada će minimalna koncentracija bakterija doći u jezero i kada će se u njemu moći kupati?

Rješenje Funkcija dostiže maksimum ili min kada je njen izvod nula.

,

Odredimo max ili min će biti za 6 dana. Da bismo to učinili, uzimamo drugi izvod.

Odgovor: Nakon 6 dana bit će minimalna koncentracija bakterija.