لگاریتم هایی با پایه های مختلف و توان های یکسان. فرمول های لگاریتمی لگاریتم ها راه حل هایی را مثال می زنند. لگاریتم های اعشاری و طبیعی

تعریف لگاریتم

لگاریتم b به پایه a، توانی است که a باید به آن افزایش یابد تا b به دست آید.

شماره eدر ریاضیات مرسوم است که حدی را که یک عبارت برای رسیدن به آن تلاش می کند، مشخص می کند

شماره eاست عدد گنگ- عددی غیرقابل قیاس با یک، نمی توان آن را دقیقاً به صورت عدد صحیح یا کسری بیان کرد. گویاعدد.

حرف ه- حرف اول یک کلمه لاتین توضیح دهنده- برای خودنمایی، از این رو نام آن در ریاضیات است نمایی- تابع نمایی

عدد هبه طور گسترده در ریاضیات و در همه علومی که به نوعی از محاسبات ریاضی برای نیازهای خود استفاده می کنند استفاده می شود.

لگاریتم ها خواص لگاریتم ها

تعریف: لگاریتم عدد مثبتمبنا b توان c است که برای بدست آوردن عدد b باید عدد a را به آن افزایش داد.

هویت لگاریتمی پایه:

7) فرمول انتقال به پایگاه جدید:

lna = log e a, e ≈ 2.718…

مسائل و تست های مبحث لگاریتم. خواص لگاریتم"

• لگاریتم - مباحث مهم برای بررسی آزمون دولتی واحد در ریاضیات

برای انجام موفقیت آمیز وظایف در مورد این موضوع، باید تعریف لگاریتم، ویژگی های لگاریتم، هویت لگاریتمی پایه، تعاریف لگاریتم اعشاری و طبیعی را بدانید. انواع اصلی مشکلات در این موضوع، مسائل مربوط به محاسبه و تبدیل عبارات لگاریتمی است. بیایید با استفاده از مثال های زیر راه حل آنها را در نظر بگیریم.

راه حل:با استفاده از خواص لگاریتم، به دست می آوریم

راه حل:با استفاده از خواص درجات به دست می آوریم

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

خواص لگاریتم ها، فرمول ها و برهان ها.

لگاریتم ها تعدادی دارند خواص مشخصه. در این مقاله به بررسی اصلی خواهیم پرداخت خواص لگاریتم ها. در اینجا فرمول های آنها را ارائه می دهیم، خواص لگاریتم ها را در قالب فرمول می نویسیم، نمونه هایی از کاربرد آنها را نشان می دهیم و همچنین اثبات خواص لگاریتم را ارائه می دهیم.

پیمایش صفحه.

خواص اصلی لگاریتم ها، فرمول ها

برای سهولت به خاطر سپردن و استفاده، بیایید تصور کنیم ویژگی های اساسی لگاریتم هادر قالب لیستی از فرمول ها در پاراگراف بعدی فرمول بندی، شواهد، مصادیق کاربرد و توضیحات لازم را بیان خواهیم کرد.

ویژگی لگاریتم یک ضریب: ، جایی که a>0، a≠1، x>0، y>0.

نتیجه: ، جایی که a>0، a≠1، n - عدد طبیعی، بزرگتر از یک، b>0.

نتیجه 1: , a>0 , a≠1 , b>0 , b≠1 .

نتیجه 2: ، a>0، a≠1، b>0، p و q اعداد واقعی هستند، q≠0، به ویژه برای b=a که داریم .

فرمولاسیون و اثبات خواص

ما به فرمول و اثبات خصوصیات نوشتاری لگاریتم ها می پردازیم. تمام خصوصیات لگاریتم بر اساس تعریف لگاریتم و هویت لگاریتمی اصلی که از آن به دست می آید و همچنین ویژگی های درجه ثابت می شود.

بیا شروع کنیم با خواص لگاریتم یک. فرمول آن به شرح زیر است: لگاریتم وحدت برابر با صفر، به این معنا که، 1=0 را ثبت کنیدبرای هر a>0، a≠1. اثبات کار دشواری نیست: از آنجایی که 0 = 1 برای هر a که شرایط فوق را ارضا می کند a>0 و a≠1، پس ثبت تساوی a 1=0 که باید ثابت شود بلافاصله از تعریف لگاریتم تبعیت می کند.

اجازه دهید مثال هایی از کاربرد خاصیت در نظر گرفته شده ارائه دهیم: log 3 1=0، log1=0 و .

بیایید به ملک بعدی برویم: لگاریتم یک عدد برابر با پایه برابر با یک ، به این معنا که، ورود a=1برای a>0، a≠1. در واقع، از آنجایی که a 1 =a برای هر a، پس طبق تعریف لگاریتم log a=1 است.

نمونه هایی از استفاده از این ویژگی لگاریتم برابری های log 5 5=1، log 5.6 5.6 و lne=1 هستند.

لگاریتم توان یک عدد برابر با پایه لگاریتم برابر است با توان. این ویژگی لگاریتم با فرمولی از فرم مطابقت دارد log a a p =p، که در آن a>0، a≠1 و p - هر عدد واقعی. این ویژگی مستقیماً از تعریف لگاریتم ناشی می شود. توجه داشته باشید که در صورت امکان نشان دادن عدد زیر علامت لگاریتم به عنوان توان پایه به شما امکان می دهد بلافاصله مقدار لگاریتم را نشان دهید؛ در مقاله محاسبه لگاریتم بیشتر در این مورد صحبت خواهیم کرد.

به عنوان مثال، log 2 2 7 =7، log10 -4 =-4 و .

لگاریتم حاصل ضرب دو عدد مثبت x و y برابر است با حاصل ضرب لگاریتم این اعداد: log a (x y)=log a x+log a y, a>0 , a≠1 . بیایید خاصیت لگاریتم یک محصول را ثابت کنیم. با توجه به ویژگی های درجه a log a x+log a y =a log a x ·a log a y، و از آنجایی که با هویت لگاریتمی اصلی یک log a x =x و یک log a y =y، پس یک log a x ·a log a y =x· y. بنابراین، یک log a x+log a y =x·y، که با تعریف لگاریتم، برابری در حال اثبات از آن به دست می‌آید.

بیایید مثال هایی از استفاده از ویژگی لگاریتم یک محصول را نشان دهیم: log 5 (2 3) = log 5 2 + log 5 3 و .

خاصیت لگاریتم یک محصول را می توان به حاصل ضرب عدد محدود n از اعداد مثبت x 1 , x 2 , …, x n تعمیم داد. log a (x 1 · x 2 ·…·x n) = ورود x 1 +log a x 2 +…+log a x n. این برابری بدون مشکل با استفاده از روش استقرای ریاضی قابل اثبات است.

به عنوان مثال، لگاریتم طبیعی حاصلضرب را می توان با مجموع سه لگاریتم طبیعی اعداد 4، e و.

لگاریتم ضریب دو عدد مثبت x و y برابر است با اختلاف لگاریتم این اعداد. خاصیت لگاریتم یک ضریب با فرمولی از فرم مطابقت دارد ، که در آن a>0، a≠1، x و y برخی از اعداد مثبت هستند. اعتبار این فرمول و همچنین فرمول لگاریتم یک محصول ثابت شده است: از آنجا که ، سپس با تعریف لگاریتم .

در اینجا مثالی از استفاده از این ویژگی لگاریتم آورده شده است: .

بیایید به ادامه مطلب برویم ویژگی لگاریتم توان. لگاریتم یک درجه برابر است با حاصل ضرب توان و لگاریتم مدول پایه این درجه. اجازه دهید این ویژگی لگاریتم یک توان را به صورت فرمول بنویسیم: log a b p =p·log a |b|، که در آن a>0، a≠1، b و p اعدادی هستند به طوری که درجه b p معنی دارد و b p > 0.

ابتدا این خاصیت را برای مثبت b ثابت می کنیم. هویت لگاریتمی پایه به ما این امکان را می دهد که عدد b را به صورت log a b، سپس b p =(a log a b) p نمایش دهیم و عبارت حاصل، به دلیل خاصیت توان، برابر با p·log a b است. بنابراین به برابری b p = a p·log a b می رسیم که از آن با تعریف لگاریتم نتیجه می گیریم که log a b p = p·log a b.

باقی می ماند که این خاصیت برای منفی b ثابت شود. در اینجا توجه می کنیم که عبارت log a b p برای منفی b فقط برای توان های زوج p معنی دارد (زیرا مقدار درجه b p باید بزرگتر از صفر باشد، در غیر این صورت لگاریتم معنی نخواهد داشت) و در این مورد b p =|b| پ. سپس b p =|b| p =(a log a |b|) p =a p·log a |b| ، از آنجا log a b p =p·log a |b| .

مثلا، و ln(-3) 4 =4·ln|-3|=4·ln3.

از ملک قبلی بر می آید ویژگی لگاریتم از ریشه: لگاریتم ریشه n برابر است با حاصل ضرب کسری 1/n توسط لگاریتم عبارت رادیکال، یعنی جایی که a>0، a≠1، n عدد طبیعی بزرگتر از یک است، b>0 .

اثبات بر اساس برابری است (به تعریف توان با توان کسری مراجعه کنید)، که برای هر b مثبت معتبر است، و ویژگی لگاریتم توان: .

در اینجا مثالی از استفاده از این ویژگی آورده شده است: .

حالا بیایید ثابت کنیم فرمول انتقال به یک پایه لگاریتمی جدیدنوع . برای این کار کافی است صحت log برابری c b=log a b·log c a را اثبات کنیم. هویت لگاریتمی پایه به ما این امکان را می دهد که عدد b را به صورت log a b نمایش دهیم، سپس log c b=log c a log a b را نشان دهیم. باقی مانده است که از خاصیت لگاریتم درجه استفاده کنیم: log c a log a b =log a b·log c a . این log برابری c b=log a b·log c a را ثابت می کند، به این معنی که فرمول انتقال به پایه جدید لگاریتم نیز ثابت شده است. .

بیایید چند مثال از استفاده از این خاصیت لگاریتم را نشان دهیم: and .

فرمول انتقال به یک پایه جدید به شما امکان می دهد تا به کار با لگاریتم هایی بروید که پایه "مناسب" دارند. به عنوان مثال، می توان از آن برای تغییر به لگاریتم های طبیعی یا اعشاری استفاده کرد تا بتوانید مقدار لگاریتم را از جدول لگاریتم محاسبه کنید. فرمول انتقال به یک پایه لگاریتمی جدید همچنین در برخی موارد امکان یافتن مقدار لگاریتم معین را هنگامی که مقادیر برخی از لگاریتم ها با پایه های دیگر مشخص است، می دهد.

یک مورد خاص از فرمول برای انتقال به یک پایه لگاریتمی جدید برای c=b فرم اغلب استفاده می شود. این نشان می دهد که log a b و log b a اعداد متقابل معکوس هستند. به عنوان مثال، .

همچنین اغلب از فرمول استفاده می شود که برای یافتن مقادیر لگاریتم راحت است. برای تأیید کلمات خود، نشان خواهیم داد که چگونه می توان از آن برای محاسبه مقدار لگاریتم فرم استفاده کرد. ما داریم . برای اثبات فرمول کافی است از فرمول انتقال به پایه جدید لگاریتم a استفاده کنید: .

باقی مانده است که خواص مقایسه لگاریتم ها را اثبات کنیم.

از روش مخالف استفاده کنیم. فرض کنید برای 1 > 1، 2 > 1 و 1 2 و برای 0 1، log a 1 b≤log a 2 b درست است. بر اساس ویژگی های لگاریتم، این نابرابری ها را می توان به صورت بازنویسی کرد و به ترتیب، و از آنها چنین است که به ترتیب log b a 1 ≤log b a 2 و log b a 1 ≥log b a 2. سپس توسط خواص قوا با بر همین اساسبرابری های b log b a 1 ≥b log b a 2 و b log b a 1 ≥b log b a 2 باید برآورده شوند، یعنی a 1 ≥a 2 . بنابراین به یک تناقض با شرط a 1 2 رسیدیم. این اثبات را کامل می کند.

ویژگی های اصلی لگاریتم ها

• مواد برای درس
• دانلود تمامی فرمول ها

لگاریتم ها، مانند هر اعداد، از هر نظر قابل جمع، تفریق و تبدیل هستند. اما از آنجایی که لگاریتم ها دقیقاً اعداد معمولی نیستند، در اینجا قوانینی وجود دارد که نامیده می شوند خواص اصلی.

شما قطعاً باید این قوانین را بدانید - بدون آنها نمی توان یک مشکل جدی را حل کرد. مسئله لگاریتمی. علاوه بر این، تعداد بسیار کمی از آنها وجود دارد - می توانید همه چیز را در یک روز یاد بگیرید. پس بیایید شروع کنیم.

جمع و تفریق لگاریتم

دو لگاریتم با پایه های یکسان را در نظر بگیرید: log a x و log a y. سپس می توان آنها را جمع و تفریق کرد و:

پس مجموع لگاریتم ها برابر لگاریتم حاصلضرب است و تفاوت آن برابر لگاریتم ضریب است. توجه داشته باشید: لحظه کلیدیاینجا - زمینه های یکسان. اگر دلایل متفاوت است، این قوانین کار نمی کند!

این فرمول ها به شما کمک می کند محاسبه کنید بیان لگاریتمیحتی زمانی که تک تک اجزای آن شمارش نشده باشد (به درس "لگاریتم چیست" مراجعه کنید). به نمونه ها دقت کنید و ببینید:

وظیفه. مقدار عبارت را پیدا کنید: log 6 4 + log 6 9.

از آنجایی که لگاریتم ها پایه های یکسانی دارند، از فرمول جمع استفاده می کنیم:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

وظیفه. مقدار عبارت را پیدا کنید: log 2 48 − log 2 3.

پایه ها یکسان هستند، ما از فرمول تفاوت استفاده می کنیم:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

وظیفه. مقدار عبارت را پیدا کنید: log 3 135 − log 3 5.

باز هم پایه ها یکسان هستند، بنابراین داریم:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

همانطور که می بینید، عبارات اصلی از لگاریتم های "بد" تشکیل شده اند که به طور جداگانه محاسبه نمی شوند. اما پس از تبدیل ها اعداد کاملا نرمال به دست می آید. بسیاری بر این واقعیت بنا شده اند اوراق تست. بله، عبارات شبیه به آزمون با جدیت تمام (گاهی اوقات تقریباً بدون تغییر) در آزمون یکپارچه دولت ارائه می شود.

استخراج توان از لگاریتم

حالا بیایید کار را کمی پیچیده کنیم. اگر پایه یا آرگومان لگاریتم یک توان باشد چه؟ سپس توان این درجه را می توان طبق قوانین زیر از علامت لگاریتم خارج کرد:

• log a x n = n · log a x ;
• 
• 

به راحتی می توان متوجه آن شد آخرین قانوندو مورد اول را دنبال می کند. اما به هر حال بهتر است آن را به خاطر بسپارید - در برخی موارد میزان محاسبات را به میزان قابل توجهی کاهش می دهد.

البته، اگر ODZ لگاریتم رعایت شود، همه این قوانین منطقی هستند: a > 0، a ≠ 1، x > 0. و یک چیز دیگر: یاد بگیرید که همه فرمول ها را نه تنها از چپ به راست، بلکه برعکس اعمال کنید. ، یعنی می توانید اعداد قبل از علامت لگاریتم را در خود لگاریتم وارد کنید. این چیزی است که اغلب مورد نیاز است.

وظیفه. مقدار عبارت log 7 49 6 را بیابید.

بیایید با استفاده از فرمول اول از درجه در استدلال خلاص شویم:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

وظیفه. معنی عبارت را پیدا کنید:

[کپشن عکس]

توجه داشته باشید که مخرج شامل یک لگاریتمی است که پایه و آرگومان آن توان های دقیق هستند: 16 = 2 4 ; 49 = 7 2. ما داریم:

[کپشن عکس]

فکر می کنم مثال آخر نیاز به توضیح دارد. لگاریتم ها کجا رفته اند؟ تا آخرین لحظه ما فقط با مخرج کار می کنیم. ما پایه و استدلال لگاریتم ایستاده در آنجا را به شکل توان ارائه کردیم و توان ها را خارج کردیم - کسری "سه طبقه" به دست آوردیم.

حالا بیایید به کسر اصلی نگاه کنیم. صورت و مخرج دارای یک عدد هستند: log 2 7. از آنجایی که log 2 7 ≠ 0، می توانیم کسر را کاهش دهیم - 2/4 در مخرج باقی می ماند. با توجه به قواعد حساب، چهار را می توان به صورتگر منتقل کرد، کاری که انجام شد. نتیجه این شد: 2.

انتقال به یک پایه جدید

در مورد قوانین جمع و تفریق لگاریتم ها، من به طور خاص تأکید کردم که آنها فقط با پایه های مشابه کار می کنند. اگر دلایل متفاوت باشد چه؟ اگر آنها قدرت های دقیق یکسان نباشند چه؟

فرمول های انتقال به یک بنیاد جدید به کمک می آیند. اجازه دهید آنها را در قالب یک قضیه فرموله کنیم:

اجازه دهید لاگ لگاریتمی a x داده شود. سپس برای هر عدد c به طوری که c > 0 و c ≠ 1، برابری درست است:

[کپشن عکس]

به طور خاص، اگر c = x را تنظیم کنیم، به دست می آید:

[کپشن عکس]

از فرمول دوم برمی‌آید که پایه و آرگومان لگاریتم را می‌توان عوض کرد، اما در این حالت کل عبارت «برگردانده می‌شود»، یعنی. لگاریتم در مخرج ظاهر می شود.

این فرمول ها به ندرت در معمولی یافت می شوند عبارات عددی. ارزیابی اینکه چقدر راحت هستند فقط با تصمیم گیری امکان پذیر است معادلات لگاریتمیو نابرابری ها

با این حال، مشکلاتی وجود دارد که به هیچ وجه نمی توان آنها را حل کرد، مگر با حرکت به یک پایه جدید. بیایید به چند مورد از این موارد نگاه کنیم:

وظیفه. مقدار عبارت را پیدا کنید: log 5 16 log 2 25.

توجه داشته باشید که آرگومان های هر دو لگاریتم دارای توان های دقیق هستند. بیایید نشانگرها را برداریم: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

حالا بیایید لگاریتم دوم را "معکوس" کنیم:

[کپشن عکس]

از آنجایی که حاصلضرب هنگام تنظیم مجدد فاکتورها تغییر نمی کند، ما با آرامش چهار و دو را ضرب کردیم و سپس با لگاریتم ها برخورد کردیم.

وظیفه. مقدار عبارت را پیدا کنید: log 9 100 lg 3.

پایه و آرگومان لگاریتم اول توانهای دقیق هستند. بیایید این را بنویسیم و از شر شاخص ها خلاص شویم:

[کپشن عکس]

حالا بیایید با حرکت به یک پایه جدید از شر لگاریتم اعشاری خلاص شویم:

[کپشن عکس]

هویت لگاریتمی پایه

اغلب در فرآیند حل، لازم است یک عدد به عنوان لگاریتم به یک پایه معین نشان داده شود. در این مورد، فرمول های زیر به ما کمک می کند:

1. n = ورود a a n

2. در حالت اول، عدد n به توان آرگومان تبدیل می شود. عدد n می تواند مطلقاً هر چیزی باشد، زیرا فقط یک مقدار لگاریتمی است.

   فرمول دوم در واقع یک تعریف بازنویسی شده است. این همان چیزی است که به آن می گویند: هویت لگاریتمی اساسی.

   در واقع اگر عدد b به قدری افزایش یابد که عدد b به این توان عدد a را بدهد چه اتفاقی می افتد؟ درست است: نتیجه همان عدد a است. این پاراگراف را دوباره با دقت بخوانید - بسیاری از مردم در آن گیر می کنند.

   مانند فرمول های انتقال به یک پایه جدید، هویت لگاریتمی پایه گاهی اوقات تنها راه حل ممکن است.

   [کپشن عکس]

   توجه داشته باشید که log 25 64 = log 5 8 - ما به سادگی مربع را از پایه و آرگومان لگاریتم گرفتیم. با در نظر گرفتن قوانین ضرب توان با پایه یکسان، به دست می آوریم:

   [کپشن عکس]

   اگر کسی نمی داند، این یک کار واقعی از آزمون یکپارچه دولتی بود :)

   واحد لگاریتمی و صفر لگاریتمی

   در پایان، من دو هویت را ارائه خواهم داد که به سختی می توان آنها را ویژگی نامید - بلکه آنها پیامدهای تعریف لگاریتم هستند. آنها دائماً در مشکلات ظاهر می شوند و در کمال تعجب حتی برای دانش آموزان "پیشرفته" نیز مشکل ایجاد می کنند.

   1. log a a = 1 یک واحد لگاریتمی است. یک بار برای همیشه به یاد داشته باشید: لگاریتم به هر پایه a از خود آن پایه برابر با یک است.
   2. log a 1 = 0 صفر لگاریتمی است. پایه a می تواند هر چیزی باشد، اما اگر آرگومان دارای یک باشد، لگاریتم برابر با صفر است! زیرا 0 = 1 نتیجه مستقیم تعریف است.

   این همه خواص است. حتما تمرین کنید که آنها را عملی کنید! برگه تقلب را در ابتدای درس دانلود کرده و پرینت بگیرید و مشکلات را حل کنید.

   لگاریتم. ویژگی های لگاریتم (جمع و تفریق).

   ویژگی های لگاریتماز تعریف آن پیروی کنید. و به این ترتیب لگاریتم عدد ببر اساس آبه عنوان توانی تعریف می شود که یک عدد باید به آن افزایش یابد آبرای دریافت شماره ب(لگاریتم فقط برای اعداد مثبت وجود دارد).

   از این فرمول نتیجه می شود که محاسبه x=log a b، معادل حل معادله است a x =b.مثلا، گزارش 2 8 = 3زیرا 8 = 2 3 . فرمول لگاریتم این امکان را فراهم می کند که اگر b=a c، سپس لگاریتم عدد ببر اساس آبرابر است با. همچنین واضح است که مبحث لگاریتم ارتباط تنگاتنگی با مبحث توان ها دارد.

   با لگاریتم، مانند هر اعداد، می توانید انجام دهید عملیات جمع، تفریقو به هر طریق ممکن متحول شود. اما با توجه به اینکه لگاریتم ها اعداد کاملاً معمولی نیستند، قوانین خاص خود را در اینجا اعمال می کنند که به آنها می گویند. خواص اصلی.

   جمع و تفریق لگاریتم.

   بیایید دو لگاریتم با پایه های یکسان بگیریم: x را ثبت کنیدو ورود به سیستم یک y. سپس می توان عملیات جمع و تفریق را انجام داد:

   همانطور که می بینیم، مجموع لگاریتم هابرابر است با لگاریتم محصول و تفاوت لگاریتم ها- لگاریتم ضریب. علاوه بر این، این درست است اگر اعداد آ، ایکسو درمثبت و a ≠ 1.

   توجه به این نکته ضروری است که جنبه اصلی در این فرمول ها همان پایه ها هستند. اگر زمینه ها متفاوت است، این قوانین اعمال نمی شود!

   قوانین جمع و تفریق لگاریتم با پایه های یکسان نه تنها از چپ به راست، بلکه برعکس نیز خوانده می شود. در نتیجه قضایای لگاریتم حاصلضرب و لگاریتم ضریب را داریم.

   لگاریتم محصولدو عدد مثبت برابر با مجموعلگاریتم های آنها ; با بیان مجدد این قضیه در صورت اعداد به صورت زیر می رسیم آ, ایکسو درمثبت و a ≠ 1، این که:

   لگاریتم ضریبدو عدد مثبت برابر است با اختلاف لگاریتم تقسیم کننده و مقسوم علیه. به بیان دیگر، اگر اعداد آ, ایکسو درمثبت و a ≠ 1، این که:

   اجازه دهید قضایای فوق را برای حل اعمال کنیم مثال ها:

   اگر اعداد ایکسو درپس منفی هستند فرمول لگاریتم محصولبی معنی می شود بنابراین، نوشتن ممنوع است:

   از آنجایی که عبارات log 2 (-8) و log 2 (-4) اصلاً تعریف نشده اند (تابع لگاریتمی در= ثبت 2 ایکسفقط برای مقادیر آرگومان مثبت تعریف شده است ایکس).

   قضیه محصولقابل اجرا نه تنها برای دو، بلکه برای تعداد نامحدودی از عوامل. این بدان معناست که برای هر طبیعی کو هر عدد مثبت ایکس 1 , ایکس 2 , . . . ,x nیک هویت وجود دارد:

   از جانب قضیه ضریب لگاریتمییک ویژگی دیگر از لگاریتم را می توان به دست آورد. این دانش عمومی است که ورود به سیستم آ 1 = 0، بنابراین

   این به این معنی است که یک برابری وجود دارد:

   لگاریتم دو عدد متقابلبه همین دلیل صرفاً با علامت با یکدیگر متفاوت خواهند بود. بنابراین:

   لگاریتم. خواص لگاریتم ها

   لگاریتم. خواص لگاریتم ها

   بیایید برابری را در نظر بگیریم. به ما اجازه دهید ارزش های و و و ما می خواهیم برای پیدا کردن ارزش.

   یعنی ما به دنبال توانی هستیم که برای به دست آوردن آن باید آن را خنثی کنیم.

   اجازه دهید یک متغیر می تواند هر مقدار واقعی را بگیرد، سپس محدودیت های زیر بر روی متغیرها اعمال می شود: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

   اگر مقادیر و را بدانیم و با وظیفه یافتن مجهول مواجه شویم، برای این منظور یک عملیات ریاضی معرفی می شود که به نام لگاریتم.

   برای یافتن ارزشی که می گیریم لگاریتم یک عددتوسط اساس :

   لگاریتم یک عدد به قاعده آن، توانی است که برای بدست آوردن آن باید به آن افزایش داد.

   به این معنا که هویت لگاریتمی پایه:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   در اصل یک نماد ریاضی است تعاریف لگاریتم.

   عملیات ریاضی لگاریتم معکوس عمل توان است، بنابراین خواص لگاریتم هاارتباط نزدیکی با ویژگی های درجه دارند.

   بیایید موارد اصلی را فهرست کنیم خواص لگاریتم ها:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>، 1″ title=”d1″/>

   4.

   5.

   گروه خصوصیات زیر به شما امکان می دهد توان یک عبارت را در زیر علامت لگاریتم یا ایستادن در پایه لگاریتم به شکل ضریب در مقابل علامت لگاریتم نشان دهید:

   6.

   7.

   8.

   9.

   گروه بعدی فرمول ها به شما امکان می دهد از یک لگاریتم با یک پایه معین به یک لگاریتم با یک پایه دلخواه حرکت کنید و نامیده می شود. فرمول های انتقال به یک پایه جدید:

   10.

   12. (نتیجه از اموال 11)

   

   سه ویژگی زیر به خوبی شناخته شده نیستند، اما اغلب برای حل معادلات لگاریتمی یا در ساده سازی عبارات حاوی لگاریتم استفاده می شوند:

   13.

   14.

   15.

   موارد خاص:

   — لگاریتم اعشاری

   — لگاریتم طبیعی

   هنگام ساده سازی عبارات حاوی لگاریتم، از یک رویکرد کلی استفاده می شود:

   1. معرفی اعداد اعشاریبه شکل معمولی

   2. اعداد مختلطبه عنوان کسرهای نامناسب نشان داده می شود.

   3. اعداد پایه لگاریتم و زیر علامت لگاریتم را به عوامل ساده تجزیه می کنیم.

   4. سعی می کنیم همه لگاریتم ها را به یک پایه کاهش دهیم.

   5. خواص لگاریتم ها را اعمال کنید.

   بیایید به نمونه هایی از ساده سازی عبارات حاوی لگاریتم نگاه کنیم.

   مثال 1.

   محاسبه:

   بیایید همه نماها را ساده کنیم: وظیفه ما این است که آنها را به لگاریتمی تقلیل دهیم که پایه آنها همان عدد پایه توان است.

   ==(با ویژگی 7)=(با ویژگی 6) =

   بیایید اندیکاتورهایی را که وارد عبارت اصلی کردیم جایگزین کنیم. ما گرفتیم:

   پاسخ: 5.25

   مثال 2. محاسبه کنید:

   

   بیایید همه لگاریتم ها را به پایه 6 کاهش دهیم (در این مورد، لگاریتم های مخرج کسری به صورت "مهاجرت" می کنند):

   بیایید اعداد زیر علامت لگاریتم را به عوامل ساده تجزیه کنیم:

   بیایید ویژگی های 4 و 6 را اعمال کنیم:

   بیایید جایگزین را معرفی کنیم

   ما گرفتیم:

   پاسخ 1

   لگاریتم . هویت لگاریتمی پایه

   خواص لگاریتم ها لگاریتم اعشاری. لگاریتم طبیعی

   لگاریتم عدد مثبت N به پایه (ب > 0, ب 1) توان x است که b باید به آن افزایش یابد تا N به دست آید .

   این ورودی معادل موارد زیر است: b x = N .

   مثالها: log 3 81 = 4، از آنجایی که 3 4 = 81;

   log 1/3 27 = – 3، از آنجایی که (1/3) - 3 = 3 3 = 27.

   تعریف فوق از لگاریتم را می توان به عنوان یک هویت نوشت:

   

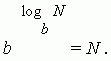
   ویژگی های اصلی لگاریتم ها

   2) log 1 = 0، از آنجا که ب 0 = 1 .

   3) لگاریتم حاصل برابر است با مجموع لگاریتم عوامل:

   4) لگاریتم ضریب برابر است با اختلاف لگاریتم تقسیم کننده و مقسوم:

   5) لگاریتم یک توان برابر است با حاصل ضرب توان و لگاریتم پایه آن:

   پیامد این خاصیت به شرح زیر است: لگاریتم ریشه برابر با لگاریتم عدد رادیکال تقسیم بر توان ریشه:

   

   6) اگر پایه لگاریتم یک درجه باشد، مقدار معکوس نشانگردرجه را می توان از علامت قافیه log خارج کرد:

   

   دو ویژگی آخر را می توان در یکی ترکیب کرد:

   

   7) فرمول مدول انتقال (یعنی انتقال از یک پایه لگاریتمی به پایه دیگر):

   

   در حالت خاصی که N=aما داریم:

   

   لگاریتم اعشاری تماس گرفت لگاریتم پایه 10. lg نشان داده می شود، i.e. ثبت 10 ن= ورود ن. لگاریتم اعداد 10، 100، 1000، . p به ترتیب 1، 2، 3، ... هستند، یعنی. موارد مثبت زیادی دارند

   واحد، چند صفر در یک عدد لگاریتمی بعد از یک وجود دارد. لگاریتم اعداد 0.1، 0.01، 0.001، . p به ترتیب –1، –2، –3، …، یعنی. به تعداد صفرهای عدد لگاریتمی قبل از یک (شامل اعداد صحیح صفر) منفی داشته باشید. لگاریتم های اعداد دیگر یک قسمت کسری دارند که به آن می گویند مانتیس. قسمت صحیح یک لگاریتم نامیده می شود مشخصه. برای استفاده عملی، لگاریتم های اعشاری راحت ترین هستند.

   لگاریتم طبیعی تماس گرفت لگاریتم پایه ه. با ln نشان داده می شود، i.e. ورود به سیستم ه ن= ورود ن. عدد هغیر منطقی است، مقدار تقریبی آن 2.718281828 است. حدی است که عدد به آن گرایش دارد (1 + 1 / n) nبا افزایش نامحدود n(سانتی متر. اولین حد فوق العادهدر صفحه "محدودیت های دنباله اعداد").
   هر چقدر هم که عجیب به نظر برسد، لگاریتم های طبیعیهنگام انجام انواع مختلف عملیات مربوط به تجزیه و تحلیل عملکرد بسیار راحت بود. محاسبه لگاریتم به پایه هبسیار سریعتر از هر دلیل دیگری انجام می شود.

• امروز برای فرزندخواندگی در روسیه چه چیزی لازم است؟ پذیرش در روسیه، علاوه بر تصمیم شخصی مسئولانه، شامل تعدادی روش برای تأیید دولتی نامزدها است. انتخاب دقیق در مرحله مقدماتی به بیشتر […]
• اطلاعات رایگان در مورد TIN یا OGRN از ثبت مالیات در سراسر روسیه - به صورت آنلاین در پورتال خدمات مالیاتی یکپارچه می توانید اطلاعاتی درباره ثبت نام ایالتی اشخاص حقوقی, کارآفرینان فردی, […]
• مجازات رانندگی بدون مدارک (گواهینامه، بیمه، STS) گاهی اوقات به دلیل فراموشی، رانندگان بدون گواهینامه پشت فرمان می نشینند و بابت رانندگی بدون مدرک جریمه می شوند. یادآور می‌شویم که یک علاقه‌مند به خودرو الزامی است که […]
• گل برای مردان. چه گل هایی می توانید به یک مرد بدهید؟ چه گل هایی می توانید به یک مرد بدهید؟ گلهای "نر" زیادی وجود ندارد، اما برخی از آنها به مردان داده می شود. یک لیست گل کوچک در مقابل شما: گل داودی. گل رز. میخک. […]
• یادداشت داخلی شکل خاصی از سند است که در محیط داخلی یک شرکت استفاده می شود و برای حل سریع مشکلات فعلی تولید خدمت می کند. معمولاً این سند با هدف معرفی برخی […]
• چه زمانی و چگونه می توان بخشی از بازنشستگی خود را از Sberbank دریافت کرد؟ Sberbank یک بانک شریک صندوق بازنشستگی دولتی است. بر این اساس، شهروندانی که برای بازنشستگی تمویل ثبت نام کرده‌اند، می‌توانند بخش تامین‌شده […]
• مزایای کودک در اولیانوفسک و منطقه اولیانوفسکدر سال 2018 علاوه بر این، همه افراد برنامه هایی را اجرا می کنند که توسط قانون فدرال تایید شده است. بیایید ببینیم چه کسی می تواند روی چه مزایایی حساب کند. چگونه مقامات منطقه […]
• راهنمای تفصیلینحوه تنظیم وکالتنامه برای نمایندگی منافع شخصیدر دادگاه در یک دعاوی مدنی یا داوری، در یک پرونده اداری یا کیفری، منافع شاکی و خوانده می تواند توسط یک وکیل نمایندگی شود: […]

ویژگی های اصلی لگاریتم طبیعی، نمودار، دامنه تعریف، مجموعه مقادیر، فرمول های پایه، مشتق، انتگرال، بسط سری توان و نمایش تابع ln x با استفاده از اعداد مختلط داده شده است.

تعریف

لگاریتم طبیعیتابع y = است ln x، معکوس به نمایی x = e y و is لگاریتمبر اساس عدد e: ln x = log e x.

لگاریتم طبیعی به طور گسترده در ریاضیات استفاده می شود زیرا مشتق آن ساده ترین شکل را دارد: (ln x)′ = 1/ x.

مستقر تعاریف، پایه لگاریتم طبیعی عدد است ه:
e ≅ 2.718281828459045...;
.

نمودار تابع y = ln x.

نمودار لگاریتم طبیعی (توابع y = ln x) بدست می آید از گرافیک نماییبازتاب آینه نسبت به خط مستقیم y = x.

لگاریتم طبیعی در تعریف شده است ارزش های مثبتمتغیر x. در دامنه تعریف خود به طور یکنواخت افزایش می یابد.

در x → 0 حد لگاریتم طبیعی منهای بی نهایت (-∞) است.

به عنوان x → + ∞، حد لگاریتم طبیعی به اضافه بی نهایت (+ ∞) است. برای x بزرگ، لگاریتم به آرامی افزایش می یابد. هر تابع توان x a با توان مثبت a سریعتر از لگاریتم رشد می کند.

خواص لگاریتم طبیعی

دامنه تعریف، مجموعه مقادیر، افراط، افزایش، کاهش

لگاریتم طبیعی تابعی است که بطور یکنواخت افزایش می یابد، بنابراین هیچ گونه افراطی ندارد. خواص اصلی لگاریتم طبیعی در جدول ارائه شده است.

مقادیر ln x

ln 1 = 0

فرمول های اصلی لگاریتم های طبیعی

فرمول های زیر از تعریف تابع معکوس:

ویژگی اصلی لگاریتم ها و پیامدهای آن

فرمول جایگزینی پایه

هر لگاریتمی را می توان بر حسب لگاریتم طبیعی با استفاده از فرمول جایگزینی پایه بیان کرد:

شواهد این فرمول ها در بخش ارائه شده است "لگاریتم".

تابع معکوس

معکوس لگاریتم طبیعی است توان.

اگر پس از آن

اگر پس از آن.

مشتق ln x

مشتق لگاریتم طبیعی:
.
مشتق لگاریتم طبیعی مدول x:
.
مشتق از مرتبه n:
.
استخراج فرمول ها > > >

انتگرال

انتگرال محاسبه می شود یکپارچه سازی توسط قطعات :
.
بنابراین،

عبارات با استفاده از اعداد مختلط

تابع متغیر مختلط z را در نظر بگیرید:
.
بیایید متغیر مختلط را بیان کنیم zاز طریق ماژول rو استدلال φ :
.
با استفاده از خواص لگاریتم، داریم:
.
یا
.
آرگومان φ منحصراً تعریف نشده است. اگر قرار دهید
، جایی که n یک عدد صحیح است،
این عدد برای n های مختلف یکسان خواهد بود.

بنابراین، لگاریتم طبیعی، به عنوان تابعی از یک متغیر مختلط، یک تابع تک مقداری نیست.

گسترش سری پاور

هنگامی که گسترش انجام می شود:

منابع:
که در. برونشتاین، ک.آ. Semendyaev، کتابچه راهنمای ریاضیات برای مهندسین و دانشجویان، "Lan"، 2009.

لگاریتم یک عدد ن بر اساس آ توان نامیده می شود ایکس ، که باید به آن بسازید آ برای دریافت شماره ن

به شرطی که
,
,

از تعریف لگاریتم چنین بر می آید که
، یعنی
- این برابری هویت لگاریتمی اساسی است.

لگاریتم های پایه 10 را لگاریتم اعشاری می نامند. بجای
نوشتن
.

لگاریتم به پایه ه طبیعی نامیده می شوند و تعیین می شوند
.

ویژگی های اصلی لگاریتم ها

لگاریتم یک برای هر پایه برابر با صفر است.

لگاریتم حاصلضرب برابر است با مجموع لگاریتم عوامل.

3) لگاریتم ضریب برابر است با اختلاف لگاریتم ها

عامل
مدول انتقال از لگاریتم به پایه نامیده می شود آ به لگاریتم در پایه ب .

با استفاده از ویژگی های 2-5، اغلب می توان لگاریتم یک عبارت پیچیده را به نتیجه عملیات ساده حسابی روی لگاریتم کاهش داد.

مثلا،

به چنین تبدیل های لگاریتمی لگاریتم می گویند. تبدیل معکوس به لگاریتم را تقویت می گویند.

فصل 2. عناصر ریاضیات عالی.

1. محدودیت ها

محدودیت عملکرد
یک عدد محدود A است اگر، به عنوان xx 0 برای هر از پیش تعیین شده
، چنین عددی وجود دارد
که به محض
، آن
.

تابعی که حدی دارد به مقدار بی نهایت کوچک با آن تفاوت دارد:
، جایی که- b.m.v.، i.e.
.

مثال. تابع را در نظر بگیرید
.

هنگام تلاش
، تابع y به سمت صفر میل می کند:

1.1. قضایای اساسی در مورد حدود

حد یک مقدار ثابت برابر با این مقدار ثابت است

.

حد مجموع (تفاوت) تعداد محدودی از توابع برابر است با مجموع (تفاوت) حدود این توابع.

حد حاصلضرب تعداد محدودی از توابع برابر است با حاصلضرب حدود این توابع.

حد نصاب دو تابع برابر است با نصاب حدود این توابع اگر حد مخرج صفر نباشد.

محدودیت های شگفت انگیز

,
، جایی که

1.2. مثال های محاسبه حد

با این حال، همه محدودیت ها به این راحتی محاسبه نمی شوند. اغلب، محاسبه حد به آشکار کردن عدم قطعیت از نوع ختم می شود: یا .

.

2. مشتق یک تابع

اجازه دهید یک تابع داشته باشیم
، پیوسته بر روی قطعه
.

بحث و جدل مقداری افزایش یافت
. سپس تابع یک افزایش دریافت می کند
.

مقدار استدلال با مقدار تابع مطابقت دارد
.

مقدار استدلال
با مقدار تابع مطابقت دارد.

از این رو، .

اجازه دهید حد این نسبت را در پیدا کنیم
. اگر این حد وجود داشته باشد، آن را مشتق تابع داده شده می نامند.

تعریف 3 مشتق تابع معین
با استدلال حد نسبت افزایش یک تابع به افزایش آرگومان، زمانی که افزایش آرگومان خودسرانه به صفر میل می کند، نامیده می شود.

مشتق از یک تابع
را می توان به صورت زیر تعیین کرد:

; ; ; .

تعریف 4عملیات یافتن مشتق تابع نامیده می شود تفکیک.

2.1. معنای مکانیکی مشتق.

بیایید حرکت مستقیم یک جسم صلب یا نقطه مادی را در نظر بگیریم.

اجازه دهید در یک نقطه از زمان نقطه متحرک
در فاصله ای بود از موقعیت شروع
.

بعد از مدتی
او فاصله ای را طی کرد
. نگرش =- سرعت متوسطنقطه مادی
. اجازه دهید با در نظر گرفتن آن، حد این نسبت را پیدا کنیم
.

در نتیجه، تعیین سرعت لحظه ای حرکت یک نقطه مادی به یافتن مشتق مسیر با توجه به زمان کاهش می یابد.

2.2. معنای هندسیمشتق

اجازه دهید یک تابع گرافیکی تعریف شده داشته باشیم
.

برنج. 1. معنای هندسی مشتق

اگر
، سپس اشاره کنید
، در امتداد منحنی حرکت می کند و به نقطه نزدیک می شود
.

از این رو
، یعنی مقدار مشتق برای مقدار معینی از آرگومان عددی برابر با مماس زاویه تشکیل شده توسط مماس در یک نقطه معین با جهت مثبت محور
.

2.3. جدول فرمول های تمایز پایه.

تابع توان

تابع نمایی

تابع لگاریتمی

تابع مثلثاتی

تابع مثلثاتی معکوس

2.4. قوانین تمایز.

مشتق از

مشتق مجموع (تفاوت) توابع

مشتق حاصل ضرب دو تابع

مشتق ضریب دو تابع

2.5. مشتق از تابع پیچیده.

اجازه دهید تابع داده شود
به گونه ای که بتوان آن را در قالب نمایش داد

و
، جایی که متغیر پس یک استدلال میانی است

مشتق تابع مختلط با حاصلضرب مشتق تابع داده شده نسبت به آرگومان میانی و مشتق آرگومان میانی نسبت به x برابر است.

مثال 1.

مثال 2.

3. تابع دیفرانسیل.

بذار باشه
، در برخی فاصله ها قابل تمایز است
رهایش کن در این تابع یک مشتق دارد

,

سپس می توانیم بنویسیم

(1),

جایی که - یک کمیت بی نهایت کوچک،

از کی تا حالا

ضرب تمام شرایط برابری (1) در
ما داریم:

جایی که
- b.m.v. مرتبه بالاتر.

اندازه
دیفرانسیل تابع نامیده می شود
و تعیین شده است

.

3.1. مقدار هندسی دیفرانسیل

اجازه دهید تابع داده شود
.

شکل 2. معنی هندسی دیفرانسیل

.

بدیهی است که دیفرانسیل تابع
برابر است با افزایش مختصات مماس در یک نقطه معین.

3.2. مشتقات و دیفرانسیل های سفارشات مختلف.

اگر آنجا
، سپس
مشتق اول نامیده می شود.

مشتق مشتق اول را مشتق مرتبه دوم می گویند و نوشته می شود
.

مشتق از مرتبه n تابع
مشتق مرتبه (n-1) ام نامیده می شود و نوشته می شود:

.

دیفرانسیل دیفرانسیل یک تابع را دیفرانسیل دوم یا دیفرانسیل مرتبه دوم می گویند.

.

.

3.3 حل مسائل بیولوژیکی با استفاده از تمایز.

وظیفه 1. مطالعات نشان داده است که رشد یک کلنی از میکروارگانیسم ها از قانون پیروی می کند
، جایی که ن - تعداد میکروارگانیسم ها (به هزار) تی - زمان (روزها).

ب) آیا جمعیت کلنی در این مدت افزایش می یابد یا کاهش می یابد؟

پاسخ. اندازه کلنی افزایش خواهد یافت.

وظیفه 2. آب دریاچه به طور دوره ای برای نظارت بر محتوای باکتری های بیماری زا آزمایش می شود. از طریق تی روز پس از آزمایش، غلظت باکتری ها با نسبت تعیین می شود

.

چه زمانی این دریاچه دارای حداقل غلظت باکتری خواهد بود و آیا می توان در آن شنا کرد؟

راه حل: یک تابع زمانی به max یا min می رسد که مشتق آن صفر باشد.

,

بیایید تعیین کنیم حداکثر یا حداقل در 6 روز خواهد بود. برای انجام این کار، بیایید مشتق دوم را در نظر بگیریم.

پاسخ: پس از 6 روز حداقل غلظت باکتری وجود خواهد داشت.