家 / いぼ/ 立方体の断面図。セクションを構築するためのタスク

立方体の断面図。セクションを構築するためのタスク

総合的な学校 I～IIIステージその2

キーロフスコエ市教育局

「立方体の平面による断面図」

そしてそれを問題に実際に応用することです。」

数学の先生が作成した

教師・方法論者

チュマコワ G.V.

2015年

導入：

多面体の断面を作成する問題は、高校の幾何学のコースと試験の両方で重要な位置を占めます。さまざまなレベル。この種の問題を解決することは、立体測定の公理の同化、知識とスキルの体系化、空間理解と構築的なスキルの開発に貢献します。セクションの構築に関する問題を解決するときに生じる困難はよく知られています。

セクションを作成する方法を構成する主なアクションは、線と平面の交点を見つけること、2 つの平面の交線を作成すること、平面に平行な直線を作成すること、直線を作成することです。平面に垂直な.

学校の数学コースの 1 つの問題を使用してセクションの構成を説明します。

№1. 立方体の少なくとも 2 つのセクションを構築しますABCDA 1 B 1 C 1 D 1 飛行機午前 1 C、点Mの場合 1 セグメント BB に沿って移動します 1 BからBへ 1 。点 M から引かれた断面の高さを測定する境界を見つけます。 1 .

解決： 点 M を使用して 2 つの必要なセクションを作成しましょう 1 点Bと点Mに近づく 2 Bに近い 1 。図には両方のセクションが示されています。 1 ちょうどB点から離れたところです 1 、断面は底辺 AC と高さ M の三角形です。 1 O、セグメント BO よりわずかに大きい、つまり
点Mの場合 1 Mの位置を取るだろう 2 点Bのすぐ近くに位置する 1 、それ 午前 2 Cはほぼ一致します AB 1 C、高さはM 1 O – セグメント B 付き 1 O、その長さは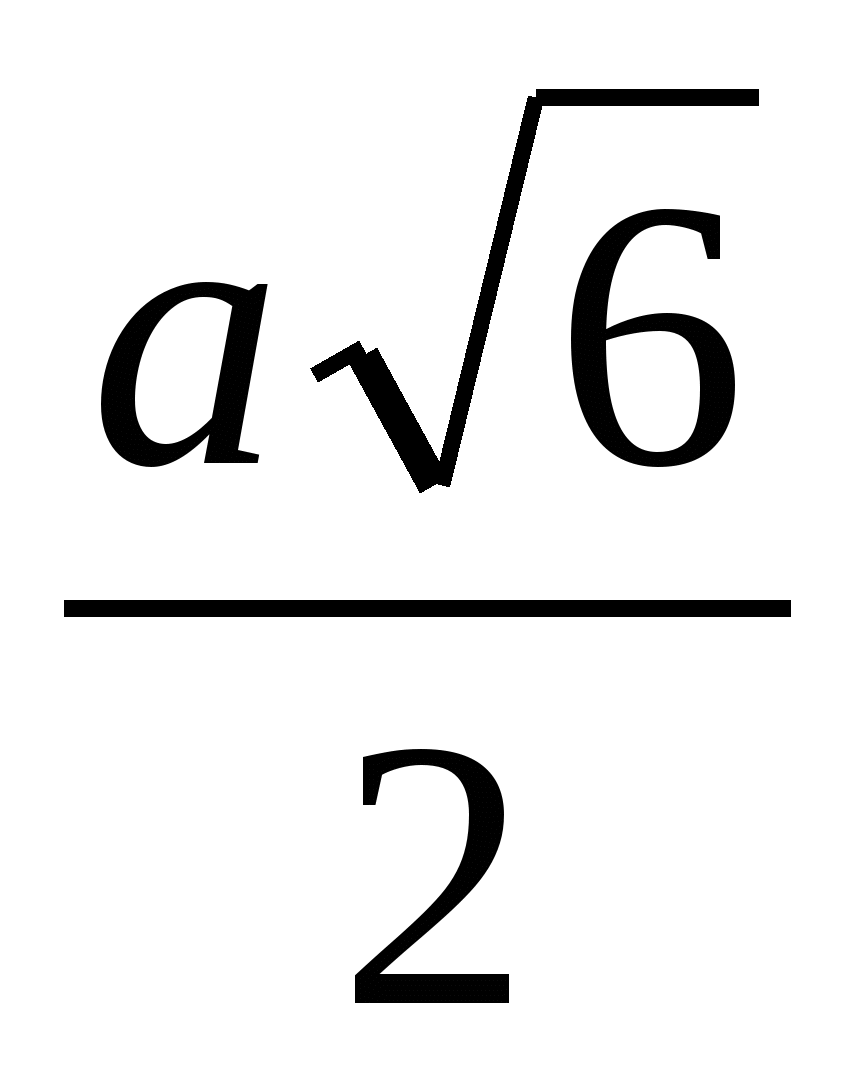
(OB1 =
=
).

ここから、継続性の理由から、次のように結論付けます。

特に点 M 1 が頂点 B の位置にある場合に何が起こるかに注目してください。

№2. 立方体の端にある 3 つの点 A 1、E、L を通る平面で立方体の断面を作成します。

面 A 1 ADD 1 と DD 1 C 1 C の平面は直線 DD 1 に沿って交差し、面 A 1 B 1 C 1 D 1 u DD 1 C 1 C の平面は直線 D 1 に沿って交差します。Ｃ１．点 A と点 E を結ぶことにより、切断面と面 AA 1 D 1 D の交点の直線が得られ、それを継続すると、切断面と面の 3 つの平面に属する点 N が見つかります。面 AA 1 D 1 D u DD 1 C 1 C の平面。

同様に、3 つの平面、つまり断面平面と面 A 1 B 1 C 1 D 1 u DD 1 C 1 C の平面に共通する点 M を見つけます。したがって、点 N u M は切断面と平面 DD 1 C 1 C に属します。直線 MN は、断面平面と面 DD 1 C 1 C の交線であり、F および K は、立方体 CD u CC 1 のエッジとの交点です。点 A 1 、 E 、 F 、 K u L を直線で一貫して接続すると、五角形 A が得られます。 EFKL を使用すると、目的のセクションが得られます。

平面を使用して立方体の断面を作成する場合バツセクション内の点を任意に配置すると、結果は三角形、台形、長方形、五角形、または六角形になります。当然のことながら、セクションのタイプがこのセクションを定義する点の位置のタイプにどのように依存するかという疑問が生じました。

それを知るために調査を行うことにしました。

1 つの頂点を持つ辺に属する 3 つの点が与えられたとき、立方体の断面を平面で構成します。

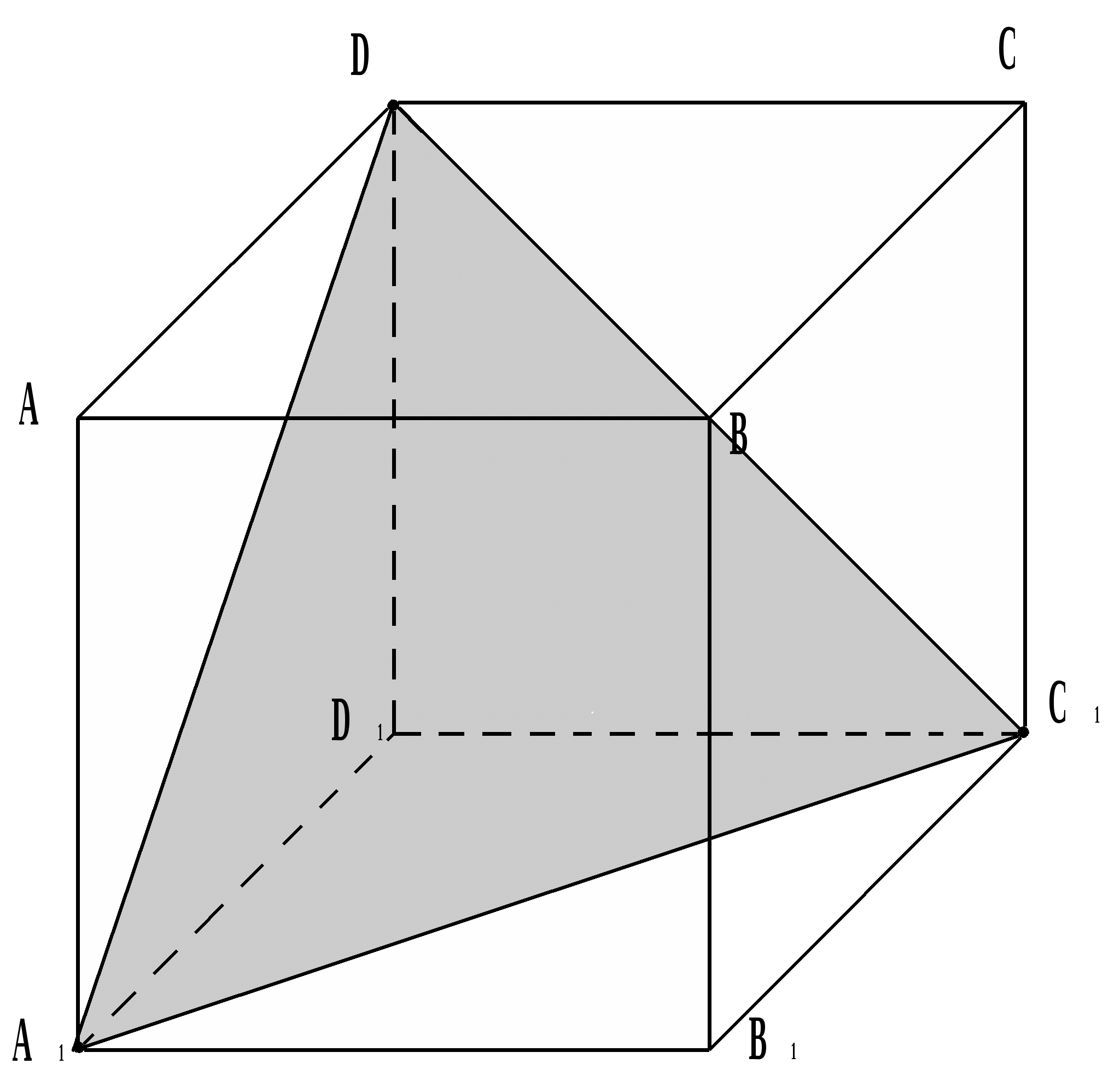
３つの点Ａ１、Ｄ、Ｃ１が取られ、これらは頂点Ｄ１に属し、それ自体が立方体の頂点である。

A 1 C 1 、A 1 D u DC 1 はこの立方体の面の対角線であるため、断面は正三角形になります。

3 つの点: A 1 u C 1 は立方体の頂点であり、点 F は立方体のエッジ DD 1 に属します。点は頂点 D 1 から出る直線に属します。

F が点 A 1 u C 1 から等距離にあるため、断面は二等辺三角形になります。

3 つの点: A 1 u C 1 は立方体の頂点であり、点 F は立方体の辺 DD 1 の直線に属します。点は、１つの頂点Ｄ１から出る直線に属する。

F が点 A 1 u C 1 から等距離にあるため、つまり LA 1 = KC 1 であるため、断面は等脚台形になります。

1 つの頂点 D 1 を持つエッジに属する 3 つの点。点ＦｕＭはそれぞれ辺Ｄ１ＤｕＤ１Ｃの延長に属し、点Ａ１は立方体の頂点である。

断面は五角形の A 1 KLNG になります。

3 つの点 F、M、Q が、それぞれエッジ D 1 D、D 1 C 1、および D 1 A 1 の継続線上に位置するように取得されます。

断面は六角形の KLNGJH になります。

3 つの点が 1 つの頂点 D 1 を持つエッジ上にあります。

断面は任意の三角形になりますが、点が D 1 Q =D 1 M =D 1 F になるように配置されている場合、つまり頂点 D 1 から等距離にある場合、断面は次のようになります。正三角形で。

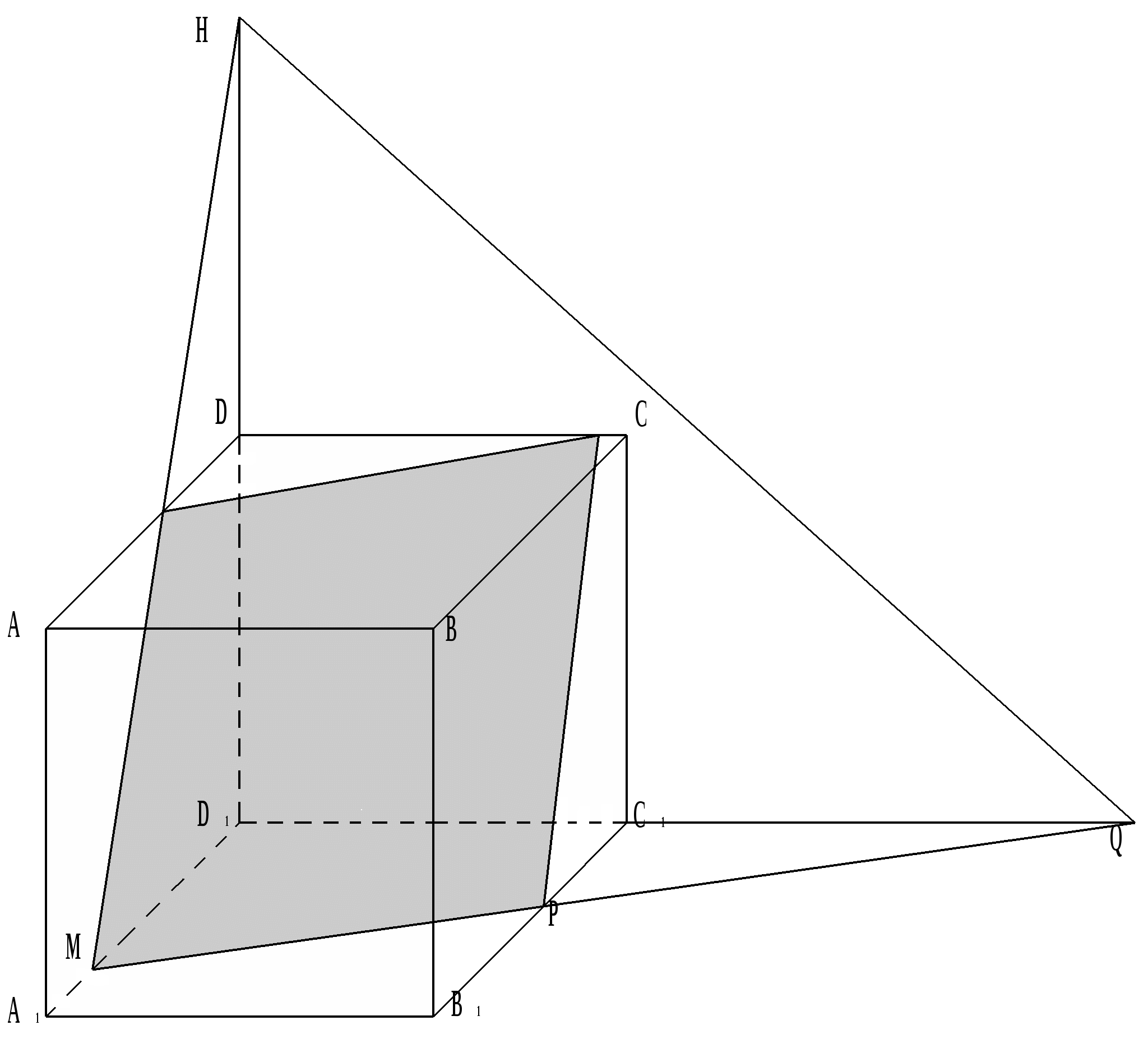
切断面は点 H、Q、M によって定義されます。 2 つの平行な平面と 3 番目の平面の交点に関する定理により、KC || MP および MK || PC であるため、断面は平行四辺形を生成します。

ポイントの場合 H、Q、M は、D から 2a の距離にある切断面を定義します。ここで、a は立方体のエッジを表し、その断面では正三角形 ACB 1 が得られます。

結論: 断面を定義する 3 つの点は、共通の頂点を持つ立方体の 3 つの辺に属するか、その連続である場合、断面は三角形、五角形、六角形、台形、平行四辺形になります。

3 つの点が与えられ、そのうちの 2 つは隣接するエッジ上にあり、3 番目の点はそれらに隣接しないエッジ上にある場合に、平面によって立方体のセクションを構築します。

3つの点Ｍ、ＫｕＦは、ＭｕＦが１つの頂点Ａ１を有するエッジに属し、点Ｋがそれらに隣接しないエッジ上に位置するように取られる。

A 1 M = D 1 K であるため、断面は長方形になります。また、3 つの垂線の定理を使用すると、MKLF が長方形であることが証明できます。 D 1 K の場合、台形または五角形が得られます。

ＫｕＬが１つの頂点Ａ１から出るエッジに属し、点ＮがエッジＣＣ１に属し、それらに隣接しないように、３つの点が取られる。エッジの中点の K、L u N、A 1 A、A 1 B 1 u CC 1 – それぞれ。

断面は正六角形になります KLGNHM

ＫｕＬが１つの頂点Ａ１から出る辺に属し、点Ｔが辺ＤＣに属するように３つの点が取られる。

断面は六角形の KLFRTZ になります。

K u L が 1 つの頂点 A 1 からの立方体の辺に属し、点 M が辺 DD 1 に属するように 3 つの点が取られます。

断面は台形の LKQM になります。

3つの点ＫｕＬは、１つの頂点Ａ１とエッジＢＣ上にある点Ｒを有するエッジに属する。

断面は五角形の KLFRT になります。

結論: 切断面が 3 つの点で定義され、そのうち 2 点が隣接するエッジ上にあり、3 点目が隣接しないエッジ上にある場合、断面は長方形、五角形、六角形、台形になります。

立方体の断面にある平行四辺形とその特殊な場合があります。

ポイントセクションを定義する T、H、J は、 T.H. 広告, H.J. 広告。断面は正方形の HTKJ になります。

セクションは点 C、F、L で指定され、DF = FD 1、BL = LB 1 となります。断面は菱形のAFCLになります。

このセクションは点 C、G、H によって定義されます。 B1H=DG。断面には、平行四辺形 A 1 GCH があります。

セクションを定義する点は、立方体 A、D、C 1 の頂点です。断面は長方形になります

立方体の断面の正多角形

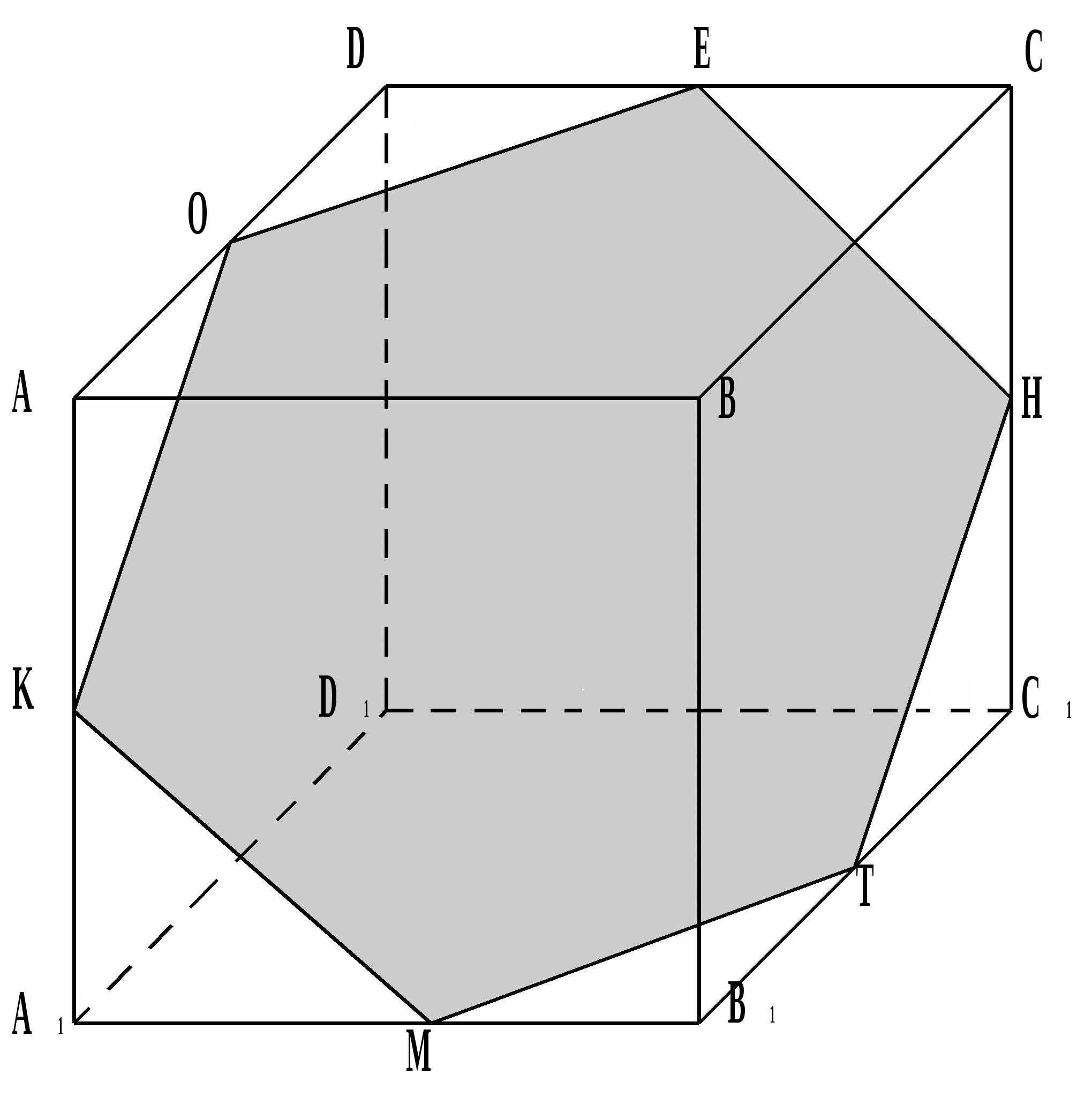
三角形 ABC 1 は、その辺が立方体の面の対角線であるため、正三角形です。

KV = MV = TV であるため、三角形 KMT は正三角形です。

断面が点 M、K、E、および MK によって定義されるため、KMTE は正方形です。広告, E.K. 広告.

断面を定義する点 H、E、K がそれぞれエッジ CC 1、DC、AA 1 の中点であるため、断面は正六角形 KMTNEO になります。

立方体と統一州試験の立体測定に関するいくつかの問題。

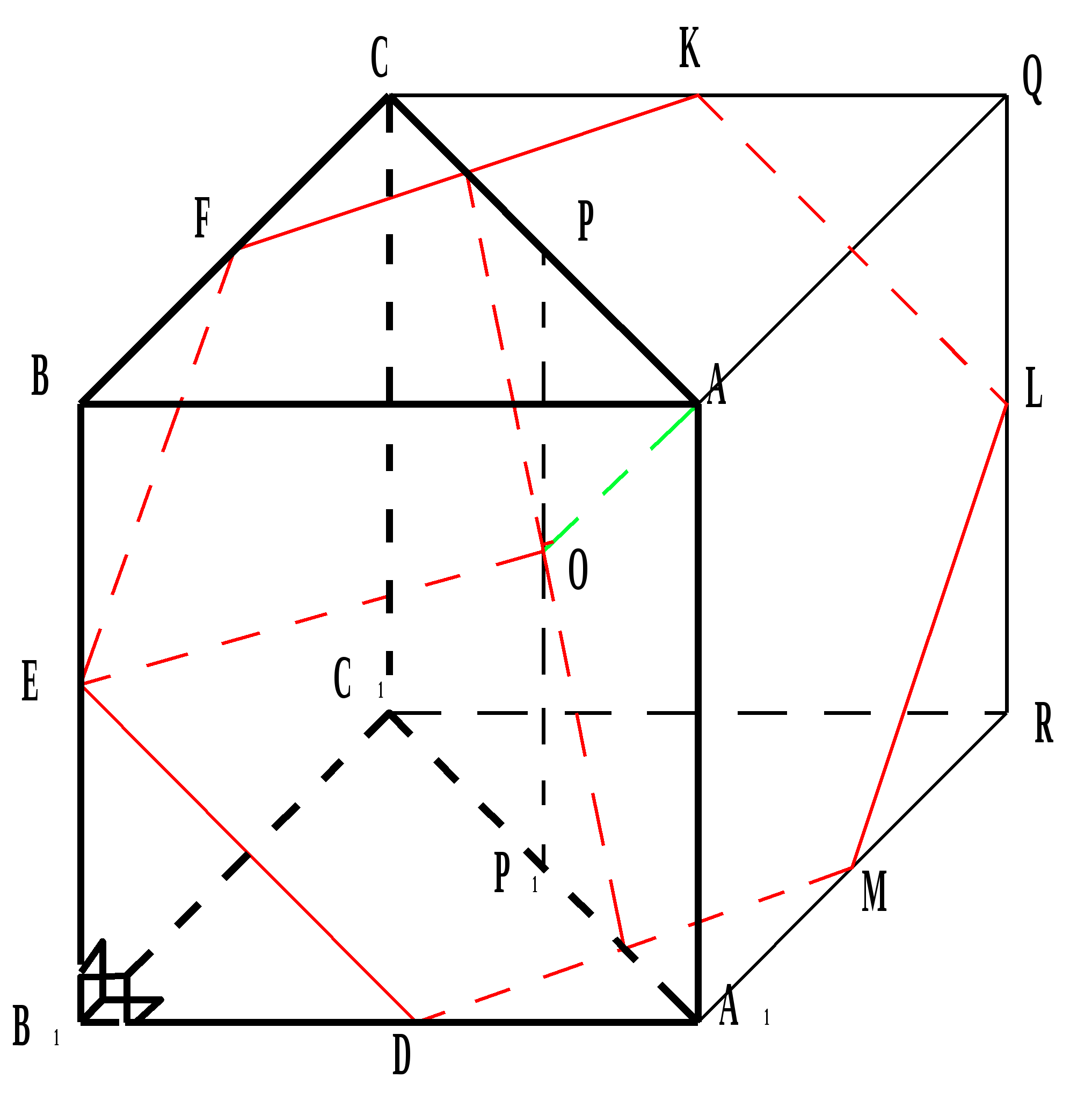
マニュアル「Unified State Exam 2005. Mathematics」に記載されています。「典型的なテスト問題」 (Kornikova T. A. et al.) 立体測定に関する 10 の問題 (C4) が含まれており、共通のアイデアによって結合されています: 三角柱 ABCA が与えられる 1 で 1 と 1 底面ABとBCの辺は互いに垂直であり、エッジBBに対して垂直です。 1 、AB=BC=BB 1 、頂点 A は円錐の頂点 (または円柱の底面の 1 つの中心、または球の中心)、円錐の底面 (球または円柱の 2 番目の底面) が中央を通過します。プリズムの一辺の長さは既知です。円錐 (球、円柱) の体積または表面を見つける必要があります。

一般的な例解決策:

このプリズムを立方体に追加します。六角形 DEFKLM - 円錐の底面による立方体の断面。その円は中央 A 1 B 1 を通過します。A は円錐の頂点、または

DEFKLM は、円柱の底面による立方体の断面であり、その円は A 1 B 1 の中心を通過します。A は円柱の 2 番目の底面の中心、または a の断面です。中心 A を持つ球の大円の平面による立方体。その球は A 1 B 1 の中心を通過します。

六角形DEFKLM– 辺 A の中央を通る平面による立方体の断面 1 で 1 、BB 1 、点を構築するときの VSZh が取得されます。K, L, M、対応するエッジの中点です。この六角形の辺は三角形の斜辺ですDB 1 E, EBF, FCK, KQL, LRM, MA 1 D、その脚は立方体の辺の半分に等しい。この場合、この六角形の中心は、その周りに外接する円の中心であり、点で立方体のエッジと交差します。D, E, F, K, LM、この円の半径
ここで、A 1 で 1 = あ .

A.O. E.L. T. に. EAL – 二等辺三角形:アル = A.E. .

( 安倍 あなた EAL– 長方形、AB= AQ= あ、なれ = L.Q. = )

EO =OL は六角形 DEFKLM の対角線 EL の中点です。つまり、AO は中央値であり、二等辺三角形の特性に従って高さになります。 AO も同様の方法で証明されます DK。 AO は六角形平面の 2 つの交差する直線に垂直であるため、AO は平面全体に垂直です。

A が円錐の頂点の場合、AO はその高さであり、A が円柱の 2 番目の底の中心の場合、AO は円柱の高さです。

ABC:AC=
, P – 立方体の底面の対角線の交点、AP=
、RR 1 =AA 1 = あ 。 OR=RR 1 = 、次に長方形から ROA JSC=
。それでAO=
.

次に、円錐について話している場合は次のようになります。

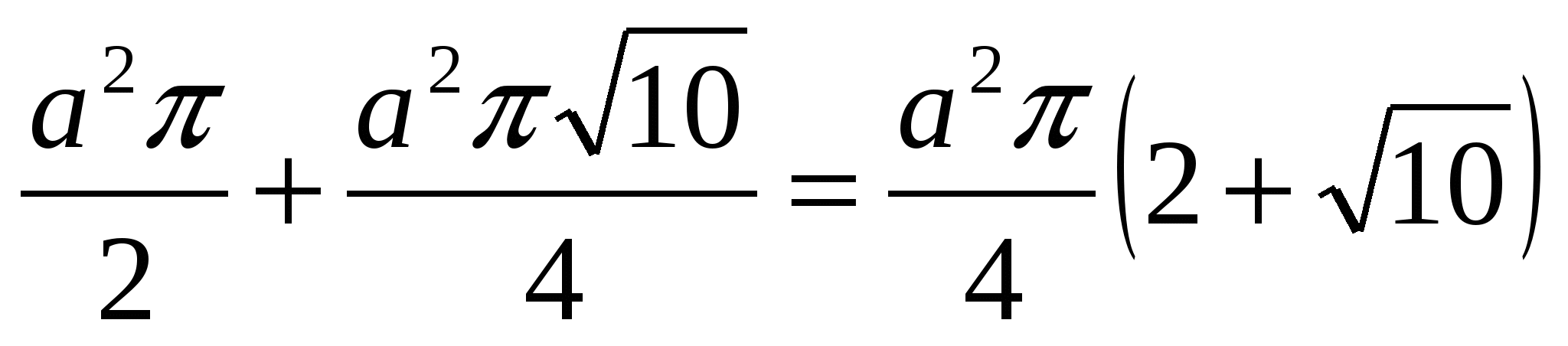
（から
).

答え：

シリンダーについて話している場合:

答え：

球体について話している場合:

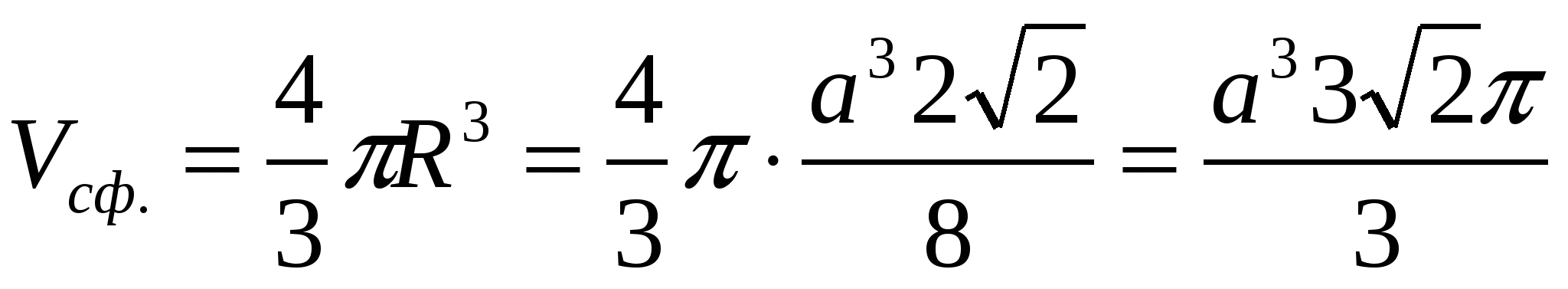
答え：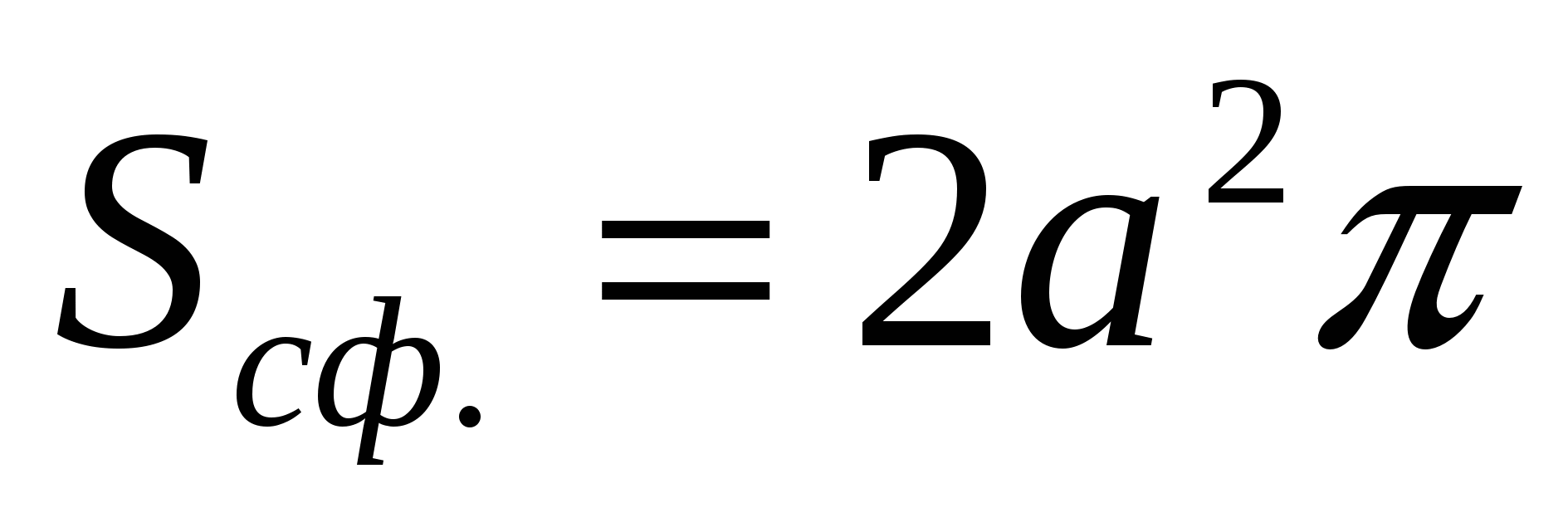

Kornikova T. A. およびその他の典型的なテストタスク。統一国家試験 - 2005 年

オプション 6。

タスク。プリズム ABCA 1 B 1 C 1 と円柱が与えられます。プリズムの底面の辺ＡＢおよびＢＣは、エッジＢＢ１に対して垂直であり、互いに垂直である。円柱の底面の中心は点 A 1 で、2 番目の底面の円はエッジ A 1 B 1 の中央を通過します。

BB 1 =AB=BC=10の場合の円柱の総表面積を求めます。その体積を求めます。

解決：

.
.

1で。 V.キューブ。レベル B。ヘルプ。平面が通過する立方体の断面を作成します。点A、K E. この平面 a) とエッジ BB1 の交線を見つけます。 b) 平面 (CC1D)。 E.C1. K.A1. D1. C.D.A.メニュー。

スライド 4プレゼンテーションから 「セクション構築に関するタスク」。プレゼンテーションを含むアーカイブのサイズは 198 KB です。

幾何学 10 年生

まとめその他のプレゼンテーション

「二面角の決定」 - エッジ上の点は任意です。 BKを作りましょう。タスク。問題解決。プレーン M. ロンバス。定義とプロパティ。どこで見られますか三の定理垂直。セグメントの終わり。ビームを発射しましょう。プロパティ。上反角ピラミッドの中で。点 M と K はさまざまな顔。セグメント AC および BC。三面体の角度のプロパティ。意味。上反角。角度を見つけてください。垂線を引きます。角度の度数。

「中心対称性の例」 - 平面。面積測定の公理。ドット。中心対称。 1 つの対称中心。ホテル「プリバルチースカヤ」。電車カプセル。セグメントの長さ。植物における対称性の例。建築における中心対称性。カモミール。セグメントには一定の長さがあります。線分。立体測定と面積測定の公理。立体測定の公理。正方形の中心対称。輸送における中心対称性。いろいろな直線。

「正多角形」 - 八面体八面体は 8 つの多角形で構成されています正三角形。「エドラ」 - 「テトラ」の面 - 4 「ヘキサ」 - 6 「オクタ」 - 8 「イコス」 - 20 「デデカ」 - 12. 四面体には 4 つの面、4 つの頂点、6 つの辺があります。十二面体には 12 の面、20 の頂点、30 の辺があります。八面体には 8 つの面、6 つの頂点、12 の辺があります。正多面体は5種類あります。十二面体十二面体は、12 個の正五角形で構成されています。

「正多面体の応用」 - 自然界の多面体。オイラーの定理。プロジェクトの目的。生活の中で使ってください。正多面体の世界。建築における多面体。芸術における多面体。数学における多面体。アルキメデス。ケプラー。多面体の理論。黄金比十二面体と二十面体で。結論。プラトン。グループ「歴史家」。ユークリッド。正多面体の出現の歴史。「黄金比」と多面体の起源の関係。

「プラトン立体」 - 八面体。プラトンの立体。六面体。正多面体。プラトン。十二面体。二元性。正二十面体。正多面体またはプラトン立体。四面体。

「多面体のセクションを構築する方法」 - 自己管理のためのルール。プリズムの断面を作成します。船。ポリゴン。最も単純なタスク。平面と多面体の相対位置。交差点。線は交差していますか? 切り込みは五角形を形成しました。カットを行います。幾何学の法則。公理的な方法。切断面の跡。タスク。切断面。多面体のセクションの構築。セクション。調査。どの飛行機でも。直方体の断面。

立方体のセクションの構築に関するタスクD1
C1
E
A1
B1
D
あ
F
B
と

検証作業。

1 オプション
オプション 2
1. 四面体
1.直方体
2. 直方体の性質

立方体の切断面とは、その両側に特定の立方体の点がある任意の平面です。

割線
平面は立方体の面と交差します
セグメント。
辺が次のような多角形
これらのセグメントは立方体のセクションと呼ばれます。
立方体の断面は三角形にすることができます。
四角形や五角形など、
六角形。
セクションを作成するときは、次のことを考慮する必要があります。
つまり、切断面が 2 つの切断面と交差する場合、
いくつかのセグメントに沿って反対側の面を配置し、
これらのセグメントは平行です。（理由を説明）。

B1
C1
D1
A1
M
K
重要！
B
と
D
切断面が交差する場合
反対側のエッジ、その後
K DCC1
それらを平行に交差させます
M BCC1
セグメント。

エッジの中点である 3 つの指定された点。エッジの場合はセクションの周囲を見つけます。

平面が通過する立方体の断面を作成します。
エッジの中点である 3 つの指定された点。
立方体の辺が a に等しい場合、断面の周囲長を求めます。
D1
N
K
A1
D
あ
C1
B1
M
と
B

与えられた 3 つの点 (頂点) を通過する平面を持つ立方体の断面を作成します。立方体のエッジの場合、断面の周囲長を見つけます。

平面が通過する立方体の断面を作成します。
その頂点である 3 つの与えられた点。探す
立方体の辺が a に等しい場合のセクションの周囲長。
D1
C1
A1
B1
D
あ
と
B

D1
C1
A1
M
B1
D
あ
と
B

指定された 3 つの点を通過する平面を持つ立方体の断面を作成します。立方体の辺が a に等しい場合、断面の周囲長を求めます。

D1
C1
A1
B1
N
D
あ
と
B

指定された 3 つの点 (エッジの中点) を通過する平面で立方体の断面を作成します。

C1
D1
B1
A1
K
D
と
N
E
あ
M
B

レッスンタイプ：複合レッスン。

目標と目的:

教育的 – 学生の空間概念の形成と発展。最も単純な多面体のセクションの構築を含む問題を解決するスキルを開発します。
教育的 - 最も単純な多面体のセクションを構築するときに、最終結果を達成するための意志と忍耐力を養います。数学を学ぶことへの愛情と興味を育みます。
現像 – 生徒の成長論理的思考、空間表現、自己制御スキルの開発。

設備：特別に開発されたプログラムを備えたコンピューター、タスクを含む既製の図面の形の配布物、多面体の立体、宿題のある個々のカード。

レッスンの構成:

レッスンのトピックと目的を述べます (2 分)。
コンピューター上でタスクを完了する方法に関する説明 (2 分)。
学生の基本的な知識とスキルを更新します (4 分)。
セルフテスト (3 分)。
教師による解き方の説明を受けながら問題を解く（15分）。
独立した仕事セルフテスト (10 分) 付き。
宿題の設定（2分）。
まとめ（2分）。

授業中

1. レッスンのトピックと目的を伝える

クラスの授業への準備状況を確認した後、教師は、今日は「多面体の断面の構築」というテーマの授業があることを報告しました。問題は、多面体の辺に属する 3 点を通過する平面を持つ単純な多面体の断面を構築することについて検討されます。多面体。パワーポイントで作成したパソコンプレゼンテーションを使用して授業を進めます。

2. コンピューター室で作業する際の安全上の注意事項

教師。私は、あなたがコンピューター教室で働き始めているという事実に注意を促します。そして、行動規則に従ってコンピューターで作業しなければなりません。格納式テーブルトップを固定し、適切にフィットするようにします。

3. 学生の基礎知識・技能の更新

教師。多面体に関連する多くの幾何学的問題を解決するには、さまざまな平面を使用して図面内でその断面を構築し、特定の線と特定の平面の交点を見つけ、特定の 2 つの平面の交線を見つけることができると便利です。。前のレッスンでは、多面体のエッジと面に平行な平面によって多面体のセクションを観察しました。このレッスンでは、多面体のエッジにある 3 つの点を通る平面でセクションを作成する問題を見ていきます。これを行うには、最も単純な多面体を考えてみましょう。この多面体は何でしょうか？（立方体、四面体、正四角錐、直角三角柱のモデルを示します。）

生徒は多面体の種類を決定する必要があります。

教師。モニター画面でどのように見えるか見てみましょう。マウスの左ボタンを押して画像から画像に移動します。

名前を付けた多面体の画像が次々と画面に表示されます。

教師。いわゆる多面体の断面を思い出してみましょう。

学生。多面体を任意の切断面で交差することによって得られる、多面体の面に属する線分を辺とし、多面体の辺に端がある多角形。

教師。どの多角形がこれらの多面体のセクションになり得るか。

学生。立方体のセクション: 3 つの六角形。四面体のセクション: 三角形、四角形。四角錐と三角柱のセクション: 3 - 五角形。

4. セルフテスト

教師。多面体の断面の概念、立体測定の公理、空間内の線と平面の相対位置の知識に従って、テスト質問に答えることが求められます。コンピュータはあなたに感謝するでしょう。最大スコアは 3 ポイント - 3 つの正解に対して。各スライドで、正解の番号が記載されたボタンをクリックする必要があります。ペアで作業するので、コンピュータが指定した同じ数のポイントを各人が受け取ります。次のスライドインジケーターをクリックします。タスクを完了するまでの時間は 3 分です。

I. 立方体の断面を平面で示した図はどれですか ABC?

II. 底面の対角線を通る平面によるピラミッドの断面を示す図はどれですか? BD端と平行に SA?

Ⅲ．点を通る四面体の断面を示す図はどれですか M平面に平行 ABS?

5. 教師による解き方の解説を受けながら問題を解く

教師。問題の解決に直接進みましょう。次のスライドインジケーターをクリックします。

タスク 1 このタスクについて、モニター画面上で段階的に構築をデモンストレーションしながら、口頭で検討します。遷移はマウスをクリックすることで実行されます。

立方体が与えられると ABCDAA 1 B 1 C 1 D 1. 彼のエッジで BB与えられた1ポイント M。線の交点を見つける C1M立方体の面の平面と あいうえお.

立方体のイメージを考えてみましょう ABCDAA 1 B 1 C 1 D 1 ドット付き M縁に BB 1ポイント Mそしてと 1 飛行機に所属している BB 1 と 1 直線について何が言えるか C1M ?

学生。真っ直ぐ C1M飛行機に属します BB 1 と 1

教師。探索した地点バツラインに属しています C1M、したがって飛行機も BB 1 と 1. それはどんな感じ相互の取り決め飛行機 BB 1 と 1と ABC?

学生。これらの平面は直線で交差します 紀元前.

教師。これは、平面のすべての共通点が BB 1 と 1と ABCラインに属している 紀元前。探索した地点バツ同時に 2 つの面の平面に属さなければなりません。 あいうえおそして BB 1 C 1 C; このことから、点 X はそれらの交線上、つまり直線上になければならないことがわかります。太陽。これは、点 X が 2 本の直線上に同時に存在する必要があることを意味します。と 1 Mそして太陽したがって、それがそれらの交差点になります。モニター画面上の任意の点の構築を見てみましょう。マウスの左ボタンを押すと、構築シーケンスが表示されます。続行します。と 1 Mそして太陽先の交差点までバツ、これは線の目的の交点です。と 1 Mフェースプレーン付き あいうえお.

教師。次のタスクに進むには、次のスライドインジケーターを使用します。構造の簡単な説明とともにこの問題を考えてみましょう。

A)点を通過する平面を持つ立方体の断面を作成します。あ 1 , MD 1 C 1と NDD 1と b)切断面と立方体の下底面の交線を見つけます。

解決。 I. 切断面には面がありますあ 1 B 1 C 1 D 1 2つの共通点あ 1と Mしたがって、これらの点を通る直線に沿って交差します。点と点を結ぶあ 1と M直線セグメントを使用して、将来の断面の平面と上面の平面の交線を見つけます。この事実を次のように書きます。あ 1 M.マウスの左ボタンを押し、もう一度押すと、この直線が作成されます。

同様に、切断面と面の交線を見つけます。 AA 1 D 1 Dそして DD 1 と 1 と。マウスボタンをクリックすると、簡単な記録と構築の進行状況が表示されます。

したがって、あ 1 ニューメキシコ州? 希望のセクションを選択します。

問題の 2 番目の部分に進みましょう。切断面と立方体の下底の平面との交線を見つけてみましょう。

II. 切断面は立方体の底面と直線で交差します。この線を描写するには、この線に属する 2 つの点を見つけるだけで十分です。切断面とフェース面の共通点 あいうえお。前の問題に基づくと、そのような点は次のようになります。バツ=。キーを押すと、短い録音と構築が表示されます。そして期間 Y、皆さんはどう思いますか、どうやって入手しますか？

学生。 Y =

教師。その構造を画面上で見てみましょう。マウスボタンをクリックします。点と点を結ぶバツそして Y（記録バツ-Y)、目的の直線、つまり切断面と立方体の下底面の交線が得られます。マウスの左ボタンを押すと、短い記録と構築が行われます。

問題 3点を通過する平面を持つ立方体の断面を作成します。

また、マウスボタンを押すと、モニター画面に建設の進行状況と短い録画が表示されます。断面の概念に基づいて、立方体の切断面と各面の平面の交線を作成するには、各面の平面内で 2 つの点を見つけるだけで十分です。ポイント Mそして N飛行機に所属しているあ 1 で 1 と 1. それらを接続すると、切断面と立方体の上面の平面の交線が得られます (マウスボタンを押します)。直線を続けましょう ミネソタ州そして D 1 C 1 交差点の前。点を取りましょうバツ、両方の平面に属しますあ 1 で 1 と 1と飛行機 DD 1 C 1 (マウスクリック)。ポイント Nそしてに飛行機に所属している BB 1 と 1. それらを結ぶと切断面と面の交線が得られます BB 1 と 1 と。 (マウスクリック)。点と点を結ぶバツそしてに, そしてそのまま直進してください HC線との交差点まで直流。点を取りましょう Rとセグメント KR –切断面と面の交線 DD 1 C 1 C。 (マウスクリック)。そのまま直進 KRそして DD 1 交差点手前でポイント獲得 Y、飛行機に属する AA 1 D 1. (マウスクリック)。この面の平面には、線の交差の結果として得られるもう 1 つの点が必要です。 ミネソタ州そしてあ 1 D 1. ここがポイントです。 (マウスクリック)。点と点を結ぶ Yそして Z、我々が得るそして。 (マウスクリック)。接続中 Qそして R, Rそして M、もらえるでしょうか？希望のセクションを選択します。

構造の簡単な説明:

2) ;

6) ;

7) ;

13) ？希望のセクションを選択します。

レッスンのトピック: セクションの構築に関するタスク。

レッスンの目的:

四面体と平行四辺形のセクションの構築を含む問題を解決するスキルを開発します。

授業中

I. 組織的な瞬間。

II. 宿題の確認

質問14、15の答え。

14. 面に 5 つの直角を持つ四面体はありますか?

(答え: いいえ、面が 4 つしかないので、それらは三角形であり、2 つの直角を持つ三角形は存在しません。)

15. 次のような平行六面体はありますか? a) 面が 1 つだけ、つまり長方形。

b) 隣接する 2 つの菱形面のみ。 c) 面のすべての角が鋭利である。 d) 面の角度はすべて直角である。 e) すべての鋭いエッジの数は、面のすべての鈍角の数と等しくありませんか?

(答え: a) いいえ (反対側は等しい)。 b) いいえ（同じ理由で）。 c) いいえ（そのような平行四辺形は存在しません）。 d) はい（直方体）。 e) いいえ (各面に 2 つの鋭角と 2 つの鈍角がある、またはすべて直線がある)。

Ⅲ．新しい教材の学習

理論的な部分。実践的な部分。理論的な部分。

多くのことを解決するには幾何学的な問題四面体と平行六面体に関連付けられている場合、図面内の異なる平面でそれらの断面を描画できると便利です。断面とは、特定の図形 (つまり、四面体または平行六面体) の点が両側にある任意の平面 (切断面と呼びましょう) を意味します。切断面はセグメントに沿って四面体 (平行六面体) と交差します。これらのセグメントによって形成される多角形が図形の断面になります。四面体には 4 つの面があるため、その断面は三角形や四角形になります。直方体には 6 つの面があります。その断面は、三角形、四角形、五角形、六角形にすることができます。

平行六面体の断面を作成するとき、切断面がいくつかのセグメントに沿って 2 つの対向する面と交差する場合、これらのセグメントは平行であるという事実を考慮します (プロパティ 1、段落 11: 2 つの場合、平行面 3 番目の線が交差している場合、それらの交線は平行になります)。

断面を作成するには、切断面と四面体 (平行六面体) のエッジとの交点を作成し、同じ面上にある 2 つの作成された点を接続するセグメントを描画するだけで十分です。

四面体を平面で切って図のような四角形にできるでしょうか？

https://pandia.ru/text/78/630/images/image002_130.gif" width="626" height="287 src=">

2.2. 点を通過する平面を持つ立方体の断面を作成します。 E, F, G、立方体の端に横たわっています。

E, F, G,

ダイレクトにしましょう E.F.と示します Pとの交点広告.

と表しましょう Q線と線の交点 PGそして AB.

点と点を結びましょう Eそして Q, Fそして G.

結果として得られる台形 EFGQ希望のセクションになります。

https://pandia.ru/text/78/630/images/image004_91.gif" width="624" height="287">