Querschnitt eines Würfels. Aufgaben zum Bau eines Abschnitts

Allgemein bildende SchuleІ-ІІІ Stufen №2

Bildungsabteilung der Verwaltung der Stadt Kirowskoje

"Schnitt eines Würfels durch ein Flugzeug

und ihre praktische Anwendung in Aufgaben.

Erstellt von einem Mathematiklehrer

Lehrer-Methodologe

Chumakova G. V.

2015

Einführung:

Probleme zur Konstruktion von Polyederabschnitten nehmen sowohl im Schulgeometriekurs für Oberstufenklassen als auch in Prüfungen einen bedeutenden Platz ein. verschiedene Level. Die Lösung dieser Art von Problemen trägt zur Assimilation der Axiome der Stereometrie, zur Systematisierung von Wissen und Fähigkeiten, zur Entwicklung räumlicher Darstellung und konstruktiver Fähigkeiten bei. Schwierigkeiten, die beim Lösen von Problemen beim Bau von Abschnitten auftreten, sind bekannt.

Die Hauptaktionen, aus denen sich die Methode zum Konstruieren von Abschnitten zusammensetzt, sind das Finden des Schnittpunkts einer geraden Linie mit einer Ebene, das Erstellen von Schnittlinien zweier Ebenen, das Erstellen einer geraden Linie parallel zu einer Ebene und das Erstellen einer geraden Linie senkrecht zur Ebene.

Ich werde den Aufbau eines Abschnitts zu einem Problem aus einem Schulmathematikkurs veranschaulichen:

№1. Konstruieren Sie mindestens zwei Teile des WürfelsABCDA 1 B 1 C 1 D 1 Flugzeug AM 1 C wenn Punkt M 1 bewegt sich entlang des Segments BB 1 von B nach B 1 . Finden Sie die Grenzen der Messung der Höhe des Abschnitts, der vom Punkt M gezogen wird 1 .

Entscheidung: Wir konstruieren zwei erforderliche Abschnitte, indem wir den Punkt M nehmen 1 näher an Punkt B und Punkt M 2 näher an B 1 . Beide Abschnitte sind in der Abbildung dargestellt: Zu Beginn der Bewegung, wenn Punkt M 1 Ich habe mich gerade von Punkt B entfernt 1 , ist der Schnitt ein Dreieck mit der Basis AC und der Höhe M 1 Oh, das ist etwas größer als das Segment VO, d.h.
Wenn Punkt M 1 nimmt Position M ein 2 ganz in der Nähe von Punkt B 1 , dann BIN 2 Passt fast zu AB 1 C, und seine Höhe ist M 1 O - mit Segment B 1 O, dessen Länge ist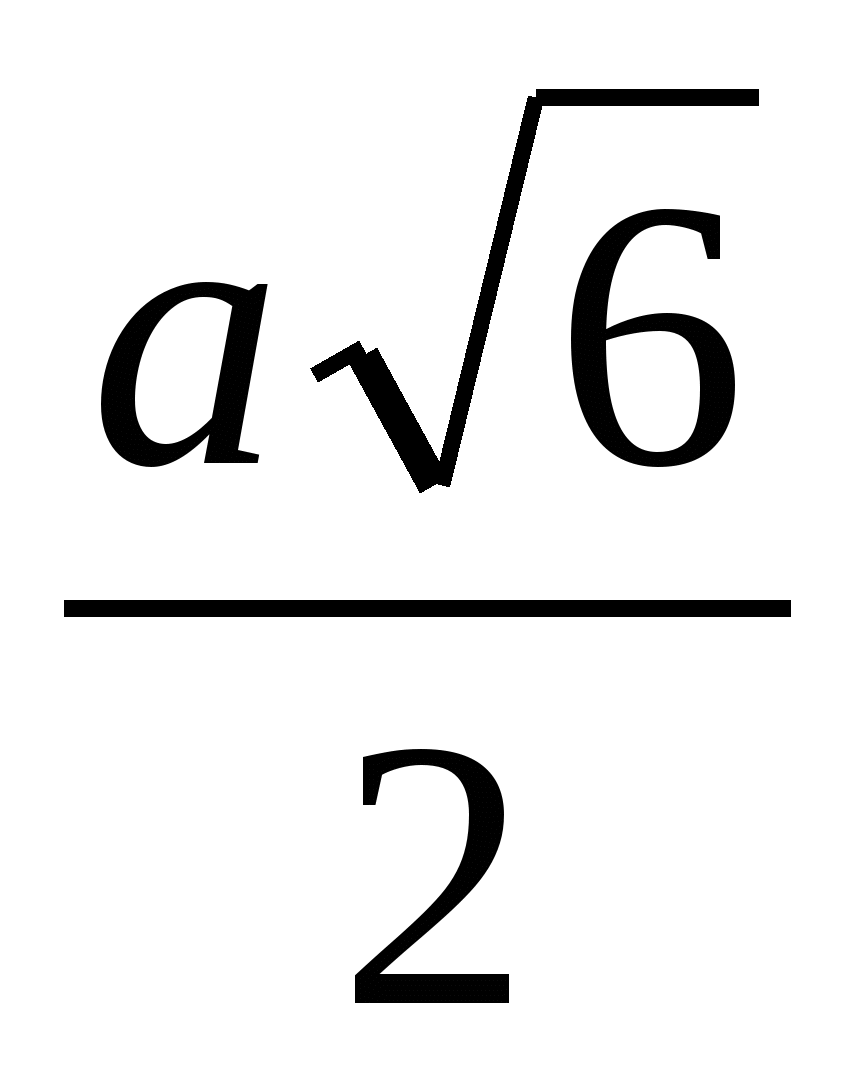
(OB 1 =
=
).

Daher schließen wir aus Gründen der Kontinuität:

Sie sollten sich vor allem anschauen, was passiert, wenn der Punkt M 1 die Position der Spitze B einnimmt.

№2. Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch drei Punkte A 1 , E und L verläuft, die auf den Kanten des Würfels liegen.

Die Ebenen der Flächen A 1 ADD 1 und DD 1 C 1 C schneiden sich entlang der geraden Linie DD 1 , und die Ebenen der Flächen A 1 B 1 C 1 D 1 u DD 1 C 1 C schneiden sich entlang der geraden Linie D 1 C1 . Wenn wir die Punkte A und E verbinden, erhalten wir die Schnittlinie der Schnittebene mit der Ebene der Fläche AA 1 D 1 D, und wenn wir sie fortsetzen, finden wir den Punkt N, der zu drei Ebenen gehört: der Schnittebene und den Ebenen der Gesichter AA 1 D 1 D u DD 1 C 1 C.

In ähnlicher Weise finden wir den Punkt M, der drei Ebenen gemeinsam ist: der Schnittebene und den Ebenen der Flächen A 1 B 1 C 1 D 1 u DD 1 C 1 C . Somit gehören die Punkte N u M zu der Schnittebene und der Ebene DD 1 C 1 C ; Gerade MN ist die Schnittlinie der Schnittebene mit der Ebene der Fläche DD 1 C 1 C , und F und K sind ihre Schnittpunkte mit den Kanten des Würfels CD u CC 1 . Verbindet man die Punkte A 1 , E , F , K u L konsequent mit Geraden, erhält man das Fünfeck A ! EFKL , die uns den erforderlichen Abschnitt liefert.

Beim Konstruieren eines Abschnitts eines Würfels durch eine Ebene X Bei einer beliebigen Anordnung von Punkten im Schnitt stellt sich heraus: ein Dreieck, ein Trapez, ein Rechteck, ein Fünfeck oder ein Sechseck. Natürlich stellte sich die Frage, wie die Art des Abschnitts von der Art der Lage der diesen Abschnitt definierenden Punkte abhängt

Ich beschloss, eine Studie durchzuführen, deren Zweck es ist, dies herauszufinden.

Konstruieren Sie Schnitte eines Würfels durch eine Ebene, wenn drei Punkte gegeben sind, die zu Kanten mit einer Ecke gehören.

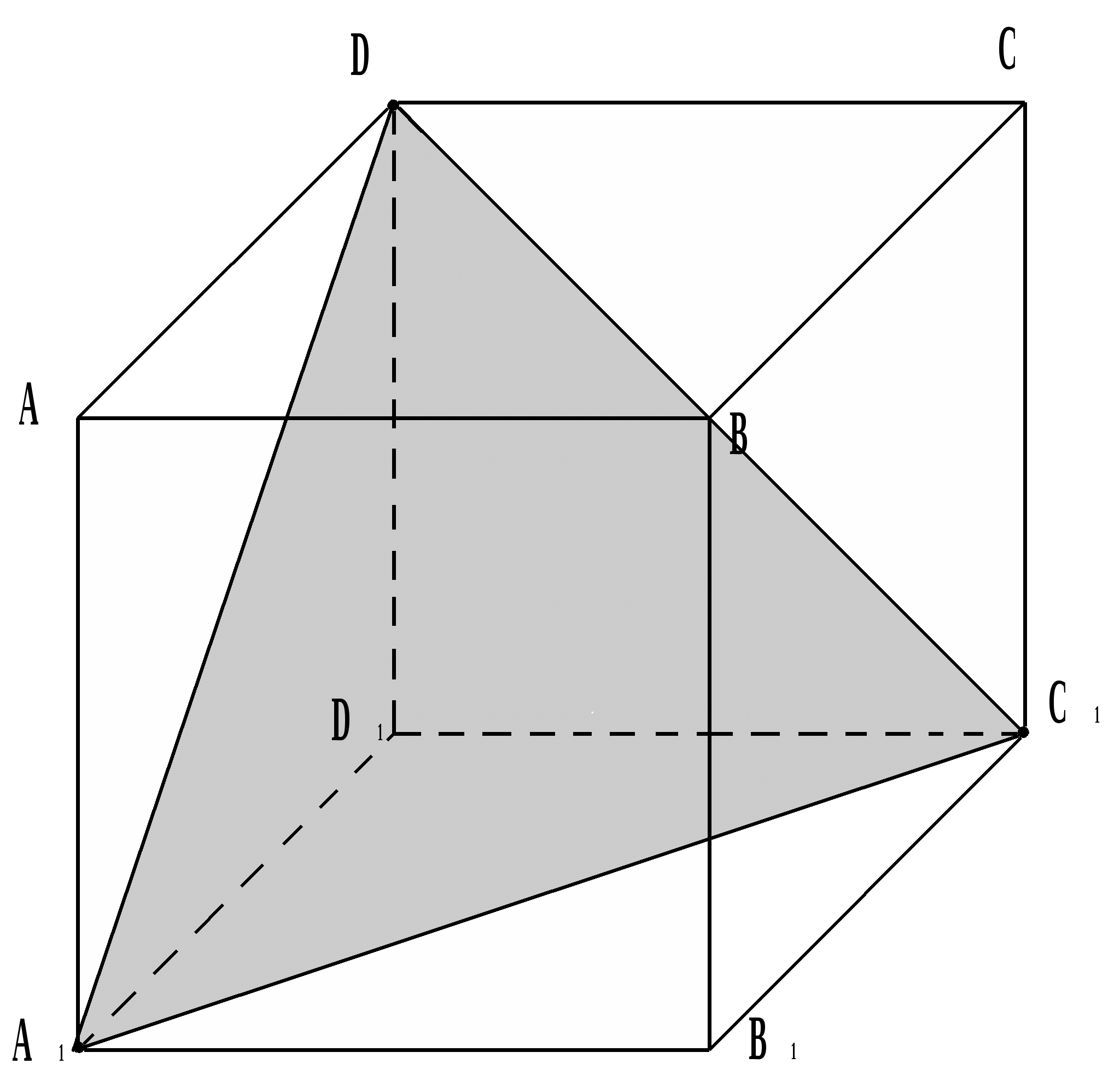
Nehmen wir drei Punkte A 1 , D , C 1 , die zur Ecke D 1 gehören und selbst die Ecken des Würfels sind.

Der Querschnitt stellte sich als gleichseitiges Dreieck heraus, da A 1 C 1 , A 1 D u DC 1 die Diagonalen der Flächen dieses Würfels sind.

Drei Punkte: A 1 u C 1 sind die Ecken des Würfels, und der Punkt F gehört zur Kante des Würfels DD 1 . Die Punkte gehören zu den Linien, die aus dem Scheitelpunkt D 1 kommen.

Der Querschnitt stellte sich als gleichschenkliges Dreieck heraus, da F von den Punkten A 1 u C 1 äquidistant ist.

Drei Punkte: A 1 u C 1 sind Ecken des Würfels, und der Punkt F gehört zur Linie der Würfelkante DD 1 . Die Punkte gehören zu geraden Linien, die aus demselben Scheitelpunkt D 1 kommen.

Im Schnitt ergibt sich ein gleichschenkliges Trapez, da F von den Punkten A 1 u C 1 äquidistant ist, also LA 1 = KC 1.

Drei Punkte, die zu Kanten mit einem Knoten D 1 gehören. Die Punkte F u M gehören jeweils zu den Verlängerungen der Kanten D 1 D u D 1 C, und der Punkt A 1 ist die Spitze des Würfels.

Der Querschnitt ist ein Fünfeck A 1 KLNG .

Drei Punkte F , M u Q werden so genommen, dass sie auf der Verlängerung der Kanten D 1 D , D 1 C 1 bzw. D 1 A 1 liegen.

Der Querschnitt ist ein Sechseck KLNGJH .

Drei Punkte liegen auf Kanten mit einem Scheitelpunkt D 1 .

Im Schnitt wurde ein beliebiges Dreieck erhalten, aber wenn die Punkte so angeordnet wären, dass D 1 Q \u003d D 1 M \u003d D 1 F, das heißt, wenn sie gleich weit vom Scheitelpunkt D 1 entfernt wären, dann wäre es ein gleichseitiges Dreieck in der Sektion erhalten.

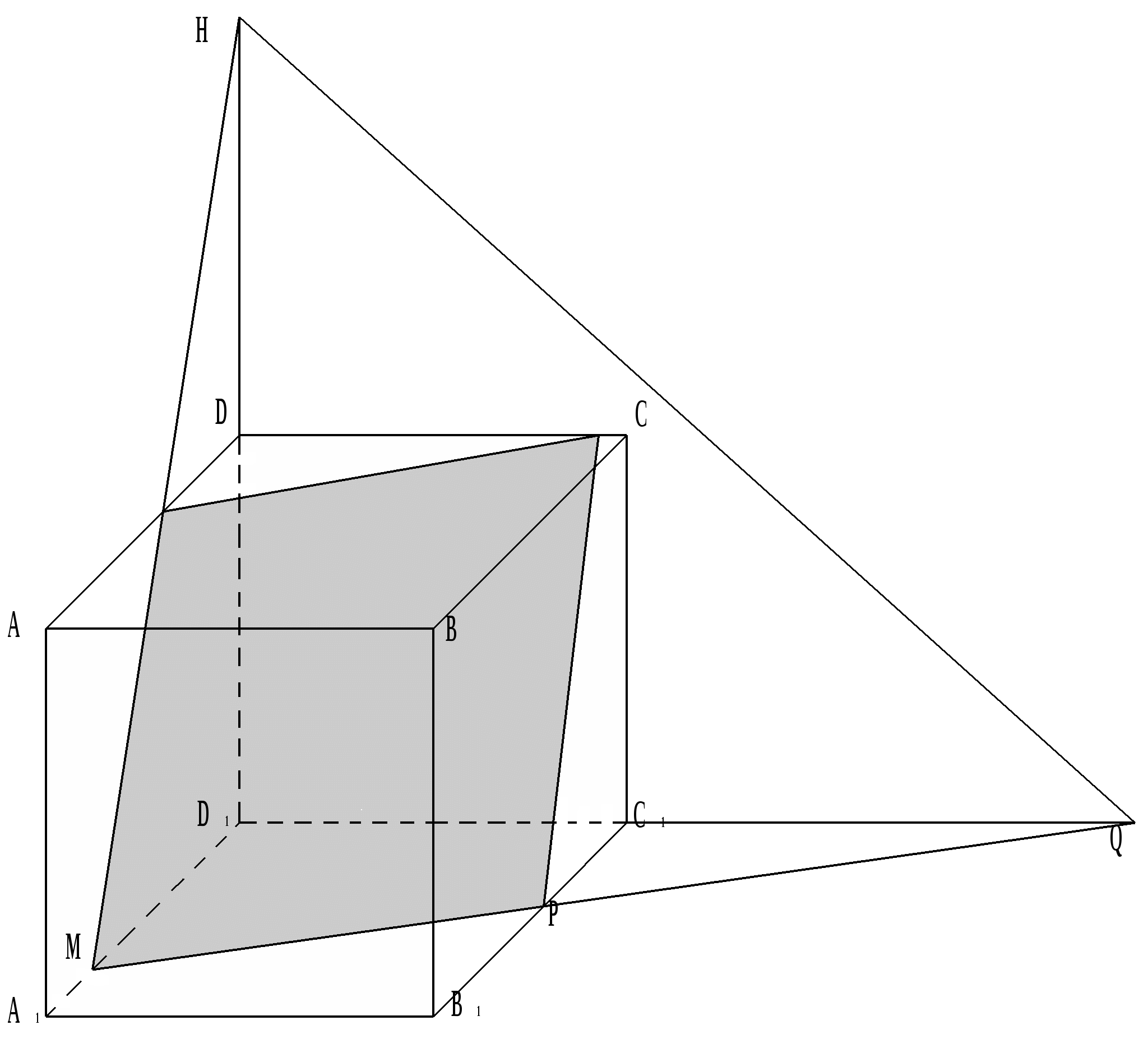
Die Schnittebene ist durch die Punkte H, Q und M gegeben. Im Schnitt ergibt sich ein Parallelogramm, da KC ││ MP und MK ││ PC, nach dem Satz vom Schnittpunkt zweier paralleler Ebenen durch die dritte.

Wenn die Punkte H, Q und M die von D entfernte Schnittebene im Abstand 2a setzen, wobei a für die Kante des Würfels steht, dann erhält man im Schnitt ein regelmäßiges Dreieck ACB 1 .

Fazit: Drei Punkte, die den Abschnitt definieren, gehören zu drei Kanten eines Würfels mit einer gemeinsamen Ecke oder sind ihre Fortsetzung, dann stellt sich im Abschnitt heraus: ein Dreieck, ein Fünfeck, ein Sechseck, ein Trapez, ein Parallelogramm.

Konstruktion eines Würfelabschnitts durch eine Ebene, wenn drei Punkte gegeben sind, von denen zwei auf benachbarten Kanten und der dritte Punkt auf einer nicht benachbarten Kante liegen.

Drei Punkte M , K u F , werden so genommen, dass M u F zu Kanten mit einem Scheitelpunkt A 1 gehören und der Punkt K auf einer Kante liegt, die nicht zu ihnen benachbart ist.

Im Schnitt wird ein Rechteck erhalten, da A 1 M \u003d D 1 K und durch den Satz über drei Senkrechte bewiesen werden kann, dass MKLF ein Rechteck ist. und wenn A 1 M D 1 K, dann kann ein Trapez oder ein Fünfeck herauskommen.

Es werden drei Punkte genommen, so dass K u L zu den Kanten gehören, die von demselben Scheitelpunkt A 1 ausgehen, und der Punkt N zu der Kante CC 1 gehört, die nicht zu ihnen benachbart ist. K , L u N sind jeweils die Mittelpunkte der Kanten A 1 A , A 1 B 1 u CC 1 .

Der Querschnitt ist ein regelmäßiges Sechseck KLGNHM

Es werden drei Punkte genommen, so dass K u L zu den Kanten gehören, die von demselben Scheitelpunkt A 1 ausgehen, und der Punkt T zu der Kante DC gehört.

Im Schnitt wird ein Sechseck KLFRTZ erhalten.

Drei Punkte werden genommen, so dass K u L zu den Kanten des Würfels von einer Ecke A 1 gehören, und der Punkt M zu der Kante DD 1 gehört.

Der Querschnitt ist ein Trapez LKQM .

Drei Punkte K u L , die zu den Kanten mit einem Knoten A 1 gehören, und dem Punkt R, der auf der Kante BC liegt.

Im Schnitt erhält man ein Fünfeck KLFRT.

Fazit: Wenn die Schnittebene durch drei Punkte gegeben ist, von denen zwei auf benachbarten Kanten liegen und der dritte auf einer nicht benachbarten Kante, dann kann der Schnitt ein Rechteck, Fünfeck, Sechseck, Trapez sein.

Ein Abschnitt eines Würfels ist ein Parallelogramm und seine Sonderfälle.

Punkte T , H , J , die den Abschnitt definieren, sind so angeordnet, dass TH ANZEIGE, HJ ANZEIGE. Im Schnitt wird ein quadratisches HTKJ erhalten.

Der Schnitt ist durch die Punkte C, F, L und DF = FD 1 , BL = LB 1 gegeben. Der Querschnitt ist ein Rhombus AFCL.

Der Schnitt ist durch die Punkte C, G, H gegeben. B 1 H = DG . Im Abschnitt des Parallelogramms A 1 GCH.

Die den Schnitt definierenden Punkte sind die Eckpunkte des Würfels A, D, C 1 . Der Querschnitt ist ein Rechteck.

Regelmäßige Polygone in einem Abschnitt eines Würfels

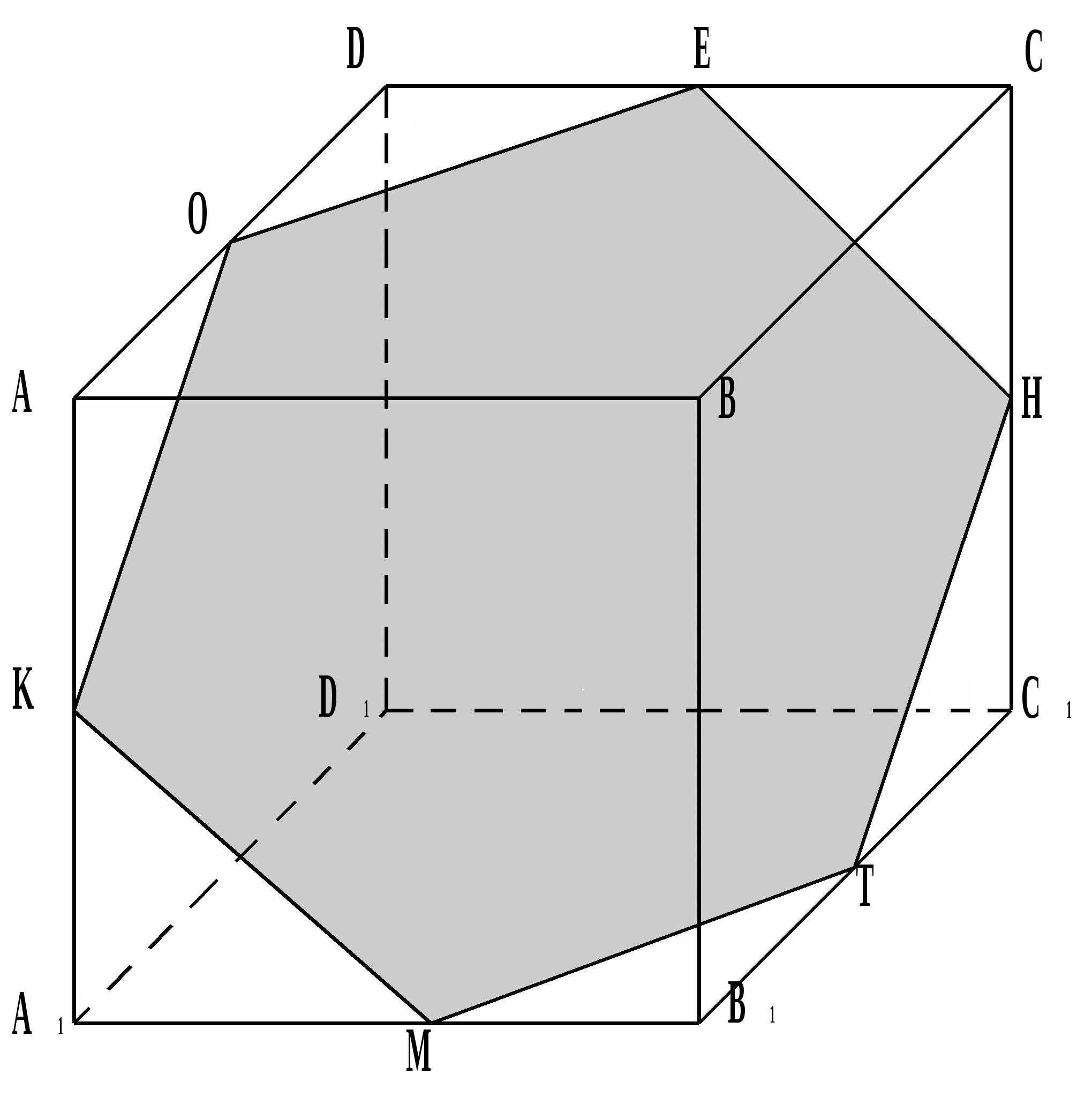
Das Dreieck ABB 1 ist gleichseitig, da seine Seiten die Diagonalen der Würfelflächen sind.

Das Dreieck KMT ist gleichseitig, da KV=MV=TV.

KMTE ist ein Quadrat, da der Schnitt durch die Punkte M, K, E und MK gegeben ist ANZEIGE, EK ANZEIGE.

Der Schnitt hat ein regelmäßiges Sechseck KMTNEO, da die den Schnitt definierenden Punkte H, E, K jeweils die Mittelpunkte der Kanten CC 1, DC, AA 1 sind.

Ein Würfel und mehrere Aufgaben in Stereometrie mit dem Einheitlichen Staatsexamen.

Im Handbuch „USE 2005. Mathematik. Typische Testaufgaben“ (Kornikova T. A. et al.) Enthält 10 Aufgaben (С4) zur Stereometrie, vereint durch eine gemeinsame Idee: Gegeben ist ein dreieckiges Prisma ABCA 1 BEIM 1 Mit 1 die Seiten der Basis AB und BC sind senkrecht zueinander und senkrecht zur Kante BB 1 , AB=BC=BB 1 , Scheitelpunkt A ist der Scheitelpunkt des Kegels (oder der Mittelpunkt einer der Grundflächen des Zylinders oder der Mittelpunkt der Kugel), geht die Grundfläche des Kegels (die Kugel oder die zweite Grundfläche des Zylinders) durch die Mitte einer Kante des Prismas, dessen Länge bekannt ist. Es ist notwendig, das Volumen oder die Oberfläche eines Kegels (Kugel, Zylinder) zu finden.

Allgemeines Beispiel Lösungen:

Fügen Sie dieses Prisma einem Würfel hinzu. Hexagon DEFKLM - ein Abschnitt eines Würfels durch die Ebene der Basis des Kegels, dessen Kreis durch die Mitte A 1 B 1 verläuft, A ist die Spitze des Kegels oder

DEFKLM ist ein Schnitt eines Würfels durch die Ebene der Grundfläche des Zylinders, dessen Umfang durch die Mitte A 1 B 1 geht, A ist der Mittelpunkt der zweiten Grundfläche des Zylinders, oder es ist ein Schnitt durch die Würfel durch die Ebene eines großen Kugelkreises mit Mittelpunkt A, dessen Kugel durch die Mitte von A 1 B 1 geht.

HexagonDEFKLM- Schnitt des Würfels durch eine Ebene, die durch die Mitte der Kanten A verläuft 1 BEIM 1 , BB 1 , VSZH beim Bauen bekommen wir PunkteK, L, M, die die Mittelpunkte der entsprechenden Kanten sind. Die Seiten dieses Sechsecks sind die Hypotenusen der DreieckeDB 1 E, EBF, FCK, KQL, LRM, MA 1 D, dessen Schenkel gleich der halben Würfelkante sind. Dann ist der Mittelpunkt dieses Sechsecks der Mittelpunkt des um ihn herum umschriebenen Kreises, der die Kanten des Würfels an Punkten schneidetD, E, F, K, Lund M der Radius dieses Kreises
, wo ein 1 BEIM 1 = a .

AO EL, t. zu. EAL - gleichschenklig:AL = AE .

( AB u EAL- rechteckig,AB= AQ= a, SEIN = LQ = )

EO \u003d OL als Mittelpunkt der Diagonale EL des Sechsecks DEFKLM, d. H. AO ist der Median und gemäß den Eigenschaften eines gleichschenkligen Dreiecks auch die Höhe. AO wird ähnlich bewiesen. DK. Da AO senkrecht zu zwei sich schneidenden Geraden der Ebene des Sechsecks steht, steht AO senkrecht zur gesamten Ebene.

Wenn A die Spitze des Kegels ist, dann ist AO seine Höhe; wenn A der Mittelpunkt der zweiten Basis des Zylinders ist, dann ist AO die Höhe des Zylinders.

ABC: AC=
, P – Schnittpunkte der Diagonalen der Würfelbasis, АР=
, RR 1 =AA 1 = a . OP=PP 1 = , dann von einem Rechteck ROA AO=
. Also AO=
.

Dann, wenn wir über einen Kegel sprechen:

=

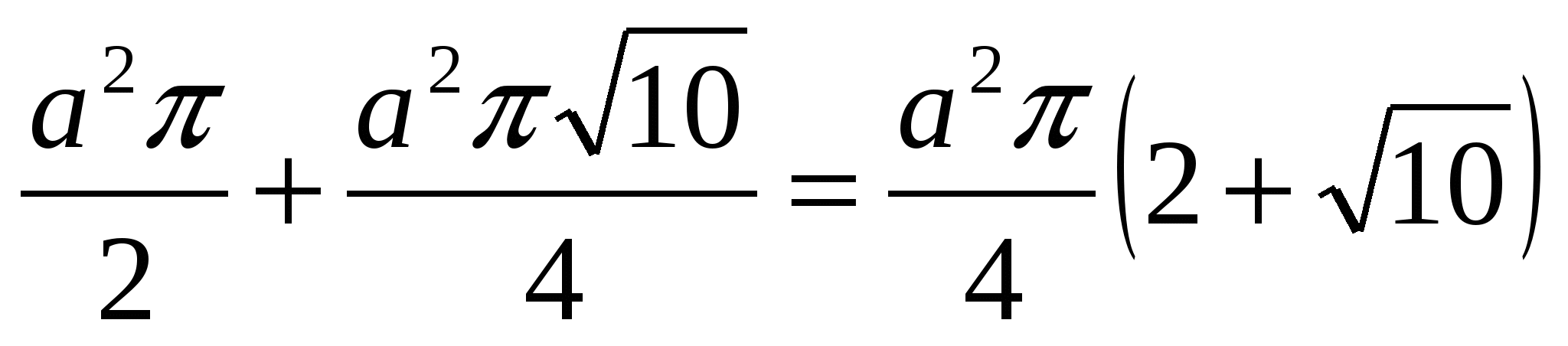
(aus
).

Antworten:

Wenn es ein Zylinder ist:

Antworten:

Wenn es um Bereiche geht:

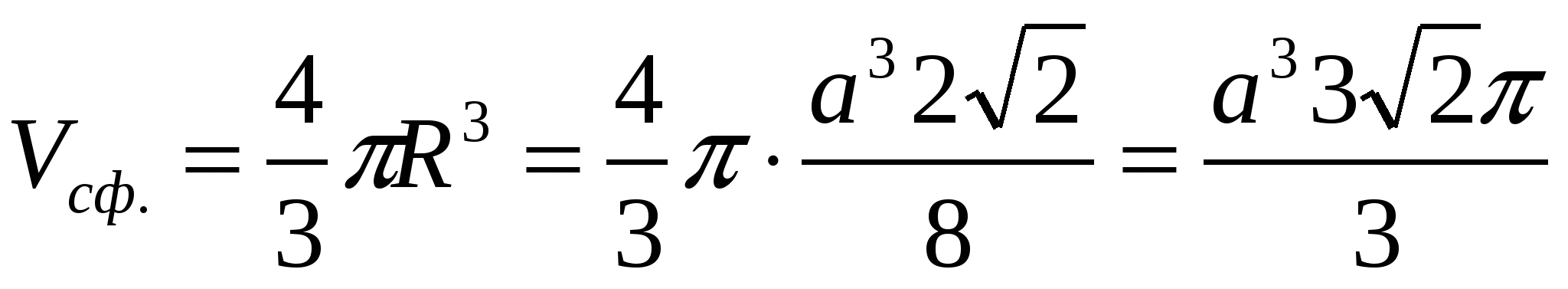
Antworten: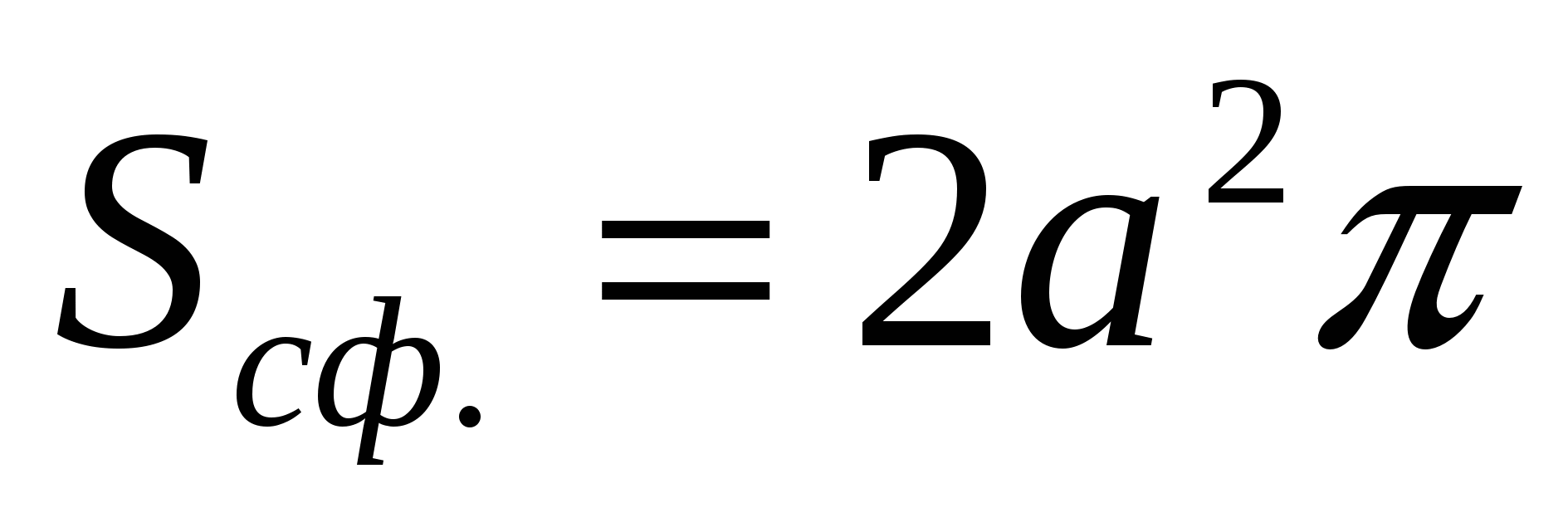

Kornikova T. A. und andere typische Testaufgaben. VERWENDUNG - 2005

Möglichkeit 6.

Aufgabe. Gegeben sei ein Prisma ABCA 1 B 1 C 1 und ein Zylinder. Die Seiten AB und BC der Basis des Prismas sind senkrecht zur Kante BB 1 und stehen senkrecht aufeinander. Der Mittelpunkt der Basis des Zylinders ist der Punkt A 1; der Kreis der zweiten Basis geht durch die Mitte der Kante A 1 B 1.

Finden Sie die Gesamtoberfläche des Zylinders, wenn BB 1 =AB=BC=10. Finde sein Volumen.

Entscheidung:

.
.

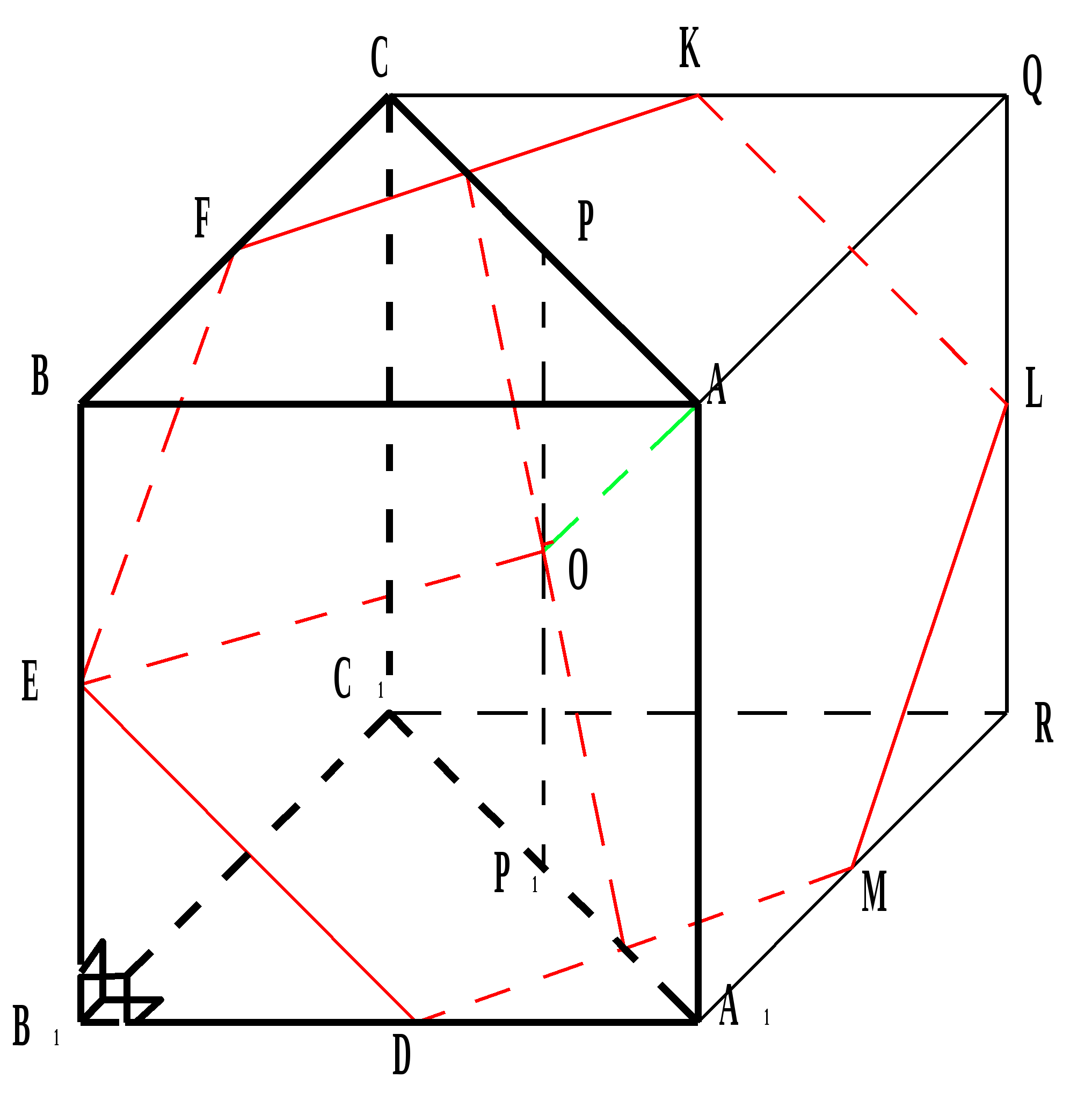
IN 1. W. Würfel Stufe B. Hilfe. Konstruieren Sie einen Abschnitt eines Würfels durch eine durchgehende Ebene Punkte A, K und E. Finden Sie die Schnittlinie dieser Ebene a) mit der Kante BB1; b) Ebene (CC1D). E. C1. K.A1. D1. C.D.A.-Menü.

Folie 4 aus der Präsentation "Probleme beim Bau von Abschnitten". Die Größe des Archivs mit der Präsentation beträgt 198 KB.

Geometrie Klasse 10

Zusammenfassung andere Präsentationen

"Ermittlung von Flächenwinkeln" - Der Punkt auf der Kante kann beliebig sein. Lassen Sie uns BK konstruieren. Aufgabe. Probleme lösen. Ebene M. Rhombus. Definition und Eigenschaften. Wo kannst du sehen Satz von drei Senkrechte. Die Enden des Segments. Nehmen wir einen Strahl. Eigenschaften. Diederwinkel in den Pyramiden. Die Punkte M und K liegen darin verschiedene Gesichter. Segmente AC und BC. Eigenschaft eines Dreikantwinkels. Definition. V-förmige Ecken. Finde eine Ecke. Zeichnen Sie eine Senkrechte. Grad Maß für einen Winkel.

"Beispiele für zentrale Symmetrie" - Ebene. Axiome der Planimetrie. Punkte. zentrale Symmetrie. Ein Symmetriezentrum. Hotel "Pribaltijskaja". Kapsel trainieren. Schnittlänge. Beispiele für Symmetrie bei Pflanzen. Zentralsymmetrie in der Architektur. Kamille. Das Segment hat eine bestimmte Länge. Liniensegment. Axiome der Stereometrie und Planimetrie. Axiome der Stereometrie. Zentralsymmetrie in Quadraten. Zentralsymmetrie im Verkehr. Verschiedene Linien.

"Gleichseitige Polygone" - Oktaeder Der Oktaeder besteht aus acht gleichseitige Dreiecke. „Hedra“ – Fläche „Tetra“ – 4 „Hexa“ – 6 „Octa“ – 8 „Ikos“ – 20 „Detek“ – 12. Ein Tetraeder hat 4 Flächen, 4 Ecken und 6 Kanten. Das Dodekaeder hat 12 Flächen, 20 Ecken und 30 Kanten. Das Oktaeder hat 8 Flächen, 6 Ecken und 12 Kanten. Es gibt 5 Arten von regelmäßigen Polyedern. Dodekaeder Der Dodekaeder besteht aus zwölf gleichseitigen Fünfecken.

"Anwendung regelmäßiger Polyeder" - Polyeder in der Natur. Satz von Euler. Projektaufgaben. Einsatz im Leben. Die Welt der regelmäßigen Polyeder. Polyeder in der Architektur. Polyeder in der Kunst. Polyeder in der Mathematik. Archimedes. Kepler. Theorie der Polyeder. Goldener Schnitt in Dodekaeder und Ikosaeder. Fazit. Plato. Historikergruppe. Euklid. Die Entstehungsgeschichte regelmäßiger Polyeder. Die Beziehung des "Goldenen Schnitts" und der Entstehung von Polyedern.

"Platos Körper" - Oktaeder. Platons Körper. Hexaeder. Regelmäßige Polyeder. Plato. Dodekaeder. Dualität. Ikosaeder. Regelmäßige Polyeder oder platonische Körper. Tetraeder.

"Methoden zum Konstruieren von Abschnitten von Polyedern" - Regeln zur Selbstkontrolle. Zeichnen Sie einen Abschnitt des Prismas. Schiff. Polygone. Die einfachsten Aufgaben. Gegenseitige Anordnung einer Ebene und eines Polyeders. Schnittpunkte. Schneiden sich die Linien? Die Schnitte bilden ein Fünfeck. Wir machen Schnitte. Die Gesetze der Geometrie. axiomatische Methode. Flugzeugspur schneiden. Aufgabe. Schnittebene. Konstruktion von Abschnitten von Polyedern. Abschnitt. Umfrage. Jedes Flugzeug. Abschnitte eines Parallelepipeds.

Aufgaben zum Erstellen von Abschnitten eines CubeD1
C1
E
A1
B1
D
SONDERN
F
B
Mit

Überprüfungsarbeit.

1 Möglichkeit
Option 2
1. Tetraeder
1. Feld
2. Eigenschaften des Parallelepipeds

Die Sekantenebene eines Würfels ist jede Ebene, auf deren beiden Seiten sich Punkte des gegebenen Würfels befinden.

Sekante
die Ebene schneidet die Flächen des Würfels
Segmente.
Ein Polygon, dessen Seiten sind
Diese Segmente werden als Abschnitt eines Würfels bezeichnet.
Die Abschnitte eines Würfels können Dreiecke sein,
Vierecke, Fünfecke u
Sechsecke.
Bei der Konstruktion von Abschnitten sollte man dies berücksichtigen
die Tatsache, dass, wenn eine Schnittebene zwei schneidet
gegenüberliegende Flächen entlang einiger Segmente
diese Segmente sind parallel. (Erkläre warum).

B1
C1
D1
A1
M
K
WICHTIG!
B
Mit
D
Wenn A die Schnittebene schneidet
gegenüberliegende Gesichter also
KDCC1
kreuzt sie parallel
MBCC1
Segmente.

drei vorgegebene Punkte, die die Mittelpunkte der Kanten sind. Finden Sie den Umfang des Abschnitts, wenn die Kante

Konstruieren Sie einen Abschnitt des Würfels durch eine durchgehende Ebene
drei vorgegebene Punkte, die die Mittelpunkte der Kanten sind.
Finden Sie den Umfang des Abschnitts, wenn die Kante des Würfels a ist.
D1
N
K
A1
D
SONDERN
C1
B1
M
Mit
B

Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch drei gegebene Punkte geht, die seine Ecken sind. Finden Sie den Umfang des Abschnitts, wenn die Kante des Würfels

Konstruieren Sie einen Abschnitt des Würfels durch eine durchgehende Ebene
drei gegebene Punkte, die seine Eckpunkte sind. Finden
der Umfang des Abschnitts, wenn die Kante des Würfels a ist.
D1
C1
A1
B1
D
SONDERN
Mit
B

D1
C1
A1
M
B1
D
SONDERN
Mit
B

Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch die drei gegebenen Punkte geht. Finden Sie den Umfang des Abschnitts, wenn die Kante des Würfels a ist.

D1
C1
A1
B1
N
D
SONDERN
Mit
B

Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch drei gegebene Punkte geht, die die Mittelpunkte seiner Kanten sind.

C1
D1
B1
A1
K
D
Mit
N
E
SONDERN
M
B

Unterrichtstyp: Kombinierter Unterricht.

Ziele und Ziele:

• lehrreich – die Bildung und Entwicklung der räumlichen Repräsentationen der Schüler; Entwicklung von Fähigkeiten zur Lösung von Problemen zum Konstruieren von Abschnitten der einfachsten Polyeder;
• lehrreich - den Willen und die Ausdauer zu kultivieren, um Endergebnisse bei der Konstruktion von Abschnitten der einfachsten Polyeder zu erzielen; Pflegen Sie Liebe und Interesse am Studium der Mathematik.
• Entwicklung – studentische Entwicklung logisches Denken, räumliche Darstellungen, Entwicklung von Selbstkontrollfähigkeiten.

Ausstattung: Computer mit einem speziell entwickelten Programm, Handouts in Form von vorgefertigten Zeichnungen mit Aufgaben, Polyederkörper, individuelle Karten mit Hausaufgaben.

Unterrichtsstruktur:

1. Über das Thema und den Zweck der Lektion berichten (2 Min.).
2. Anweisungen zum Ausführen von Aufgaben auf einem Computer (2 min).
3. Aktualisierung der grundlegenden Kenntnisse und Fähigkeiten der Schüler (4 min).
4. Prüfung mit Selbsttest (3 min).
5. Aufgaben lösen, wobei der Lehrer den Ablauf der Lösung erklärt (15 min).
6. Selbstständige Arbeit mit Selbsttest (10 min).
7. Hausaufgaben machen (2 min).
8. Zusammenfassung (2 min).

Während des Unterrichts

1. Botschaft des Themas und Zwecks der Lektion

Nachdem die Unterrichtsbereitschaft der Klasse überprüft wurde, berichtet der Lehrer, dass heute eine Unterrichtsstunde zum Thema „Konstruktion von Polyederabschnitten“ abgehalten wird, Aufgaben zum Konstruieren von Abschnitten einiger einfacher Polyeder durch Ebenen, die durch drei zu den Kanten gehörende Punkte gehen von Polyedern betrachtet werden. Der Unterricht wird anhand einer in Power Point erstellten Computerpräsentation abgehalten.

2. Sicherheitshinweise für die Arbeit in einer Computerklasse

Lehrer. Ich mache Sie darauf aufmerksam, dass Sie anfangen, in einer Computerklasse zu arbeiten, und Sie müssen die Verhaltensregeln befolgen und am Computer arbeiten. Befestigen Sie die verschiebbaren Tischplatten und stellen Sie sicher, dass sie richtig passen.

3. Aktualisierung der grundlegenden Kenntnisse und Fähigkeiten der Schüler

Lehrer. Um viele geometrische Probleme im Zusammenhang mit Polyedern zu lösen, ist es nützlich, ihre Querschnitte durch verschiedene Ebenen in der Figur erstellen zu können, den Schnittpunkt einer bestimmten Linie mit einer bestimmten Ebene zu finden und die Schnittlinie von zwei zu finden gegebene Flugzeuge. In früheren Lektionen haben wir Abschnitte von Polyedern durch Ebenen betrachtet, die parallel zu den Kanten und Flächen von Polyedern verlaufen. In dieser Lektion betrachten wir Aufgaben zum Konstruieren von Schnitten durch eine Ebene, die durch drei Punkte verläuft, die sich an den Kanten von Polyedern befinden. Betrachten Sie dazu die einfachsten Polyeder. Was sind das für Polyeder? (Modelle eines Würfels, eines Tetraeders, einer regelmäßigen viereckigen Pyramide, eines geraden dreieckigen Prismas werden demonstriert).

Die Schüler müssen die Art des Polyeders identifizieren.

Lehrer. Mal sehen, wie sie auf dem Bildschirm aussehen. Bewegen Sie sich von Bild zu Bild, indem Sie die linke Maustaste drücken.

Auf dem Bildschirm erscheinen nacheinander Bilder der benannten Polyeder.

Lehrer. Erinnern Sie sich an das, was man einen Abschnitt eines Polyeders nennt.

Student. Ein Polygon, dessen Seiten Segmente sind, die zu den Flächen des Polyeders gehören, mit Enden an den Kanten des Polyeders, das als Ergebnis des Schnitts des Polyeders mit einer beliebigen Sekantenebene erhalten wird.

Lehrer. Welche Polygone können Abschnitte dieser Polyeder sein?

Student. Abschnitte des Würfels: drei - Sechsecke. Abschnitte eines Tetraeders: Dreiecke, Vierecke. Abschnitte einer viereckigen Pyramide und eines dreieckigen Prismas: drei - Fünfecke.

4. Selbsttest

Lehrer. In Übereinstimmung mit dem Konzept eines Polyederabschnitts, der Kenntnis der Axiome der Stereometrie und der relativen Lage von Linien und Ebenen im Raum werden Sie aufgefordert, die Fragen des Tests zu beantworten. Der Computer wird Sie auswerten. Die maximale Punktzahl beträgt 3 Punkte für 3 richtige Antworten. Auf jeder Folie müssen Sie auf die Schaltfläche mit der Nummer der richtigen Antwort klicken. Sie arbeiten paarweise, so dass jeder von Ihnen die gleiche Anzahl von Punkten erhält, die der Computer anzeigt. Klicken Sie auf den Übergangszeiger zur nächsten Folie. Sie haben 3 Minuten Zeit, um die Aufgabe zu erledigen.

I. Welche Abbildung zeigt einen Schnitt eines Würfels durch eine Ebene ABC?

II. Welche Figur zeigt einen Schnitt durch eine Pyramide mit einer Ebene, die durch die Diagonale der Basis geht? BD parallel zum Rand SA?

III. Welche Abbildung zeigt einen Abschnitt eines Tetraeders, der durch einen Punkt geht M parallel zur Ebene Abs?

5. Lösen von Aufgaben mit Erläuterung des Lösungsfortschritts durch die Lehrkraft

Lehrer. Kommen wir zur Problemlösung. Klicken Sie auf den Übergangszeiger zur nächsten Folie.

Aufgabe 1 Wir betrachten diese Aufgabe mündlich mit einer schrittweisen Demonstration des Aufbaus am Bildschirm. Der Übergang erfolgt per Mausklick.

Dan-Würfel ABCDAA 1 B 1 C 1 D ein . Auf seiner Rippe BB 1 gegebener Punkt M. Finden Sie den Schnittpunkt einer Geraden C1M mit der Ebene der Würfelfläche A B C D.

Betrachten Sie ein Bild eines Würfels ABCDAA 1 B 1 C 1 D 1 mit Punkt M am Rand BB 1 Punkte M und Mit 1 gehören zum Flugzeug BB 1 Mit 1 Was lässt sich über das Direkte sagen C1M ?

Student. Gerade C1M gehört zum Flugzeug BB 1 Mit 1

Lehrer. Suchpunkt X gehört zur Linie C 1 M, und damit Flugzeuge BB 1 Mit ein . Was ist gegenseitige Übereinkunft Flugzeuge BB 1 Mit 1 und ABC?

Student. Diese Ebenen schneiden sich in einer geraden Linie BC.

Lehrer. Also alle gemeinsamen Punkte der Ebenen BB 1 Mit 1 und ABC gehören zur Linie BC. Suchpunkt X müssen gleichzeitig zu den Ebenen zweier Flächen gehören: A B C D und BB 1 C 1 C; daraus folgt, dass der Punkt X auf ihrer Schnittlinie liegen muss, also auf der Geraden Sonne. Der Punkt X muss also gleichzeitig auf zwei Geraden liegen: Mit 1 M und Sonne und damit ihr Schnittpunkt. Wir betrachten die Konstruktion des gewünschten Punktes auf dem Monitorbildschirm. Durch Drücken der linken Maustaste sehen Sie den Bauablauf: weiter Mit 1 M und Sonne vor dem Überqueren an einem Punkt X, was der erforderliche Schnittpunkt der Linie ist Mit 1 M mit Planfläche A B C D.

Lehrer. Verwenden Sie die Anzeige für die nächste Folie, um zur nächsten Aufgabe zu wechseln. Betrachten wir dieses Problem mit einer kurzen Beschreibung der Konstruktion.

a) Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch Punkte geht SONDERN 1 , MD 1 C 1 und NDD 1 und b) Finden Sie die Schnittlinie der Sekantenebene mit der Ebene der unteren Basis des Würfels.

Entscheidung. I. Die Schnittebene hat eine Fläche EIN 1 B 1 C 1 D 1 zwei gemeinsame Punkte SONDERN 1 und M und schneidet sich daher mit ihr entlang einer geraden Linie, die durch diese Punkte verläuft. Die Punkte verbinden SONDERN 1 und M Bei einem geraden Liniensegment finden wir die Schnittlinie der Ebene des zukünftigen Abschnitts und der Ebene der oberen Fläche. Wir schreiben diese Tatsache wie folgt: SONDERN 1 M. Wir drücken die linke Maustaste, diese Linie wird durch erneutes Drücken aufgebaut.

Ebenso finden wir die Schnittlinien der Sekantenebene mit den Flächen AA 1 D 1 D und DD 1 Mit 1 MIT. Durch Klicken mit der Maustaste sehen Sie eine Zusammenfassung und den Baufortschritt.

Auf diese Weise, EIN 1 NM? gewünschten Abschnitt.

Kommen wir zum zweiten Teil des Problems. Finden Sie die Schnittlinie der Sekantenebene mit der Ebene der unteren Basis des Würfels.

II. Die Sekantenebene schneidet die Ebene der Würfelbasis in einer geraden Linie. Um diese Linie darzustellen, genügt es, zwei zu dieser Linie gehörende Punkte zu finden, d.h. Gemeinsame Punkte der Schnittebene und Stirnebene A B C D. Basierend auf dem vorherigen Problem sind solche Punkte: Punkt X=. Drücken Sie die Taste, Sie sehen eine kurze Aufnahme und Gebäude. Und zeigen Y wie denkst du, wie man es bekommt?

Student. Y =

Lehrer. Schauen wir uns seine Konstruktion auf dem Bildschirm an. Drücken Sie die Maustaste. Die Punkte verbinden X und Y(Aufzeichnung X-Y) erhalten wir die gewünschte gerade Linie - die Schnittlinie der Sekantenebene mit der Ebene der unteren Basis des Würfels. Linke Maustaste drücken - kurze Aufnahme und Aufbau.

Aufgabe 3 Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch die Punkte geht:

Außerdem sehen Sie per Mausklick den Baufortschritt und ein kurzes Protokoll auf dem Monitorbildschirm. Basierend auf dem Konzept eines Schnitts reicht es für uns, zwei Punkte in der Ebene jeder Fläche zu finden, um eine Schnittlinie der Sekantenebene und der Ebene jeder Fläche des Würfels zu konstruieren. Punkte M und N gehören zum Flugzeug SONDERN 1 BEIM 1 Mit ein . Wenn wir sie verbinden, erhalten wir die Schnittlinie der Sekantenebene und der Ebene der oberen Fläche des Würfels (Maustaste drücken). Lassen Sie uns gerade Linien fortsetzen MN und D 1 C 1 vor der Kreuzung. Lassen Sie uns einen Punkt bekommen X, die zum Flugzeug gehört SONDERN 1 BEIM 1 Mit 1 und Flugzeug DD 1 C 1 (Mausklick). Punkte N und Zu gehören zum Flugzeug BB 1 Mit ein . Wenn wir sie verbinden, erhalten wir die Schnittlinie der Sekantenebene und des Gesichts BB 1 Mit 1 Mit. (Mausklick). Die Punkte verbinden X und Zu, und weiter geradeaus HC bis zum Schnittpunkt mit der Linie Gleichstrom. Lassen Sie uns einen Punkt bekommen R und segmentieren KR - Schnittlinie der Schnittebene und der Fläche DD 1 C 1 C. (Mausklick). Geradeaus weiter KR und DD 1 bis zur Kreuzung, wir bekommen einen Punkt Y zum Flugzeug gehören AA 1 D ein . (Mausklick). In der Ebene dieser Fläche benötigen wir einen weiteren Punkt, den wir durch den Schnittpunkt der Linien erhalten MN und SONDERN 1 D ein . Das ist der Punkt . (Mausklick). Die Punkte verbinden Y und Z, wir bekommen und . (Mausklick). Durch Verbinden Q und R, R und M, wir bekommen? gewünschten Abschnitt.

Kurzes Bauprotokoll:

2) ;

6) ;

7) ;

dreizehn) ? gewünschten Abschnitt.

Unterrichtsthema: Aufgaben zum Konstruieren von Abschnitten.

Das Ziel des Unterrichts:

Entwickeln Sie Fähigkeiten zur Lösung von Problemen zum Konstruieren von Abschnitten eines Tetraeders und eines Parallelogramms.

Während des Unterrichts

I. Organisatorischer Moment.

II. Überprüfung der Hausaufgaben

Antworten zu den Fragen 14, 15.

14. Gibt es einen Tetraeder mit fünf geraden Seitenwinkeln?

(Antwort: nein, weil es nur 4 Flächen gibt, es sind Dreiecke, und es gibt kein Dreieck mit zwei rechten Winkeln.)

15. Gibt es ein Parallelepiped, das hat: a) nur eine rechteckige Fläche;

b) nur zwei benachbarte Rautenflächen; c) alle Ecken der Flächen sind spitz; d) alle Ecken der Flächen sind gerade; e) die Anzahl aller scharfen Flächen ist nicht gleich der Anzahl aller stumpfen Winkel der Flächen?

(Antwort: a) nein (Gegenseiten sind gleich); b) nein (aus demselben Grund); c) nein (es gibt keine solchen Parallelogramme); d) ja (quaderförmig); e) nein (jede Fläche hat zwei spitze und zwei stumpfe Winkel, oder alle sind gerade).

III. Neues Material lernen

Theoretischer Teil. Praktischer Teil. Theoretischer Teil.

Viele zu lösen geometrische Probleme einem Tetraeder und einem Parallelepiped zugeordnet, ist es sinnvoll, ihre Schnitte in der Figur durch unterschiedliche Ebenen aufbauen zu können. Mit einem Schnitt meinen wir jede Ebene (nennen wir sie eine Schnittebene), auf deren beiden Seiten sich Punkte einer bestimmten Figur (dh eines Tetraeders oder Parallelepipeds) befinden. Die Schnittebene schneidet den Tetraeder (Parallelepiped) entlang von Segmenten. Das Polygon, das durch diese Segmente gebildet wird, ist der Schnitt der Figur. Da ein Tetraeder vier Flächen hat, kann sein Querschnitt Dreiecke und Vierecke sein. Der Quader hat sechs Seiten. Sein Querschnitt kann Dreiecke, Vierecke, Fünfecke, Sechsecke sein.

Beim Konstruieren eines Abschnitts eines Parallelepipeds berücksichtigen wir die Tatsache, dass, wenn die Schnittebene zwei gegenüberliegende Flächen entlang einiger Segmente schneidet, diese Segmente parallel sind (Eigenschaft 1, Punkt 11: Wenn zwei parallele Ebenen von der dritten gekreuzt werden, dann sind ihre Schnittlinien parallel).

Um einen Schnitt zu konstruieren, genügt es, die Schnittpunkte der Schnittebene mit den Kanten des Tetraeders (Parallelepipeds) zu konstruieren und dann Segmente zu zeichnen, die alle zwei konstruierten Punkte verbinden, die auf derselben Fläche liegen.

Kann das in der Abbildung gezeigte Viereck in einem Schnitt eines Tetraeders durch eine Ebene erhalten werden?

https://pandia.ru/text/78/630/images/image002_130.gif" width="626" height="287 src=">

2.2. Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch Punkte geht E, F, G an den Kanten des Würfels liegen.

E, F, G,

Lassen Sie uns eine gerade Linie ziehen EF und bezeichnen P seinen Schnittpunkt mit ANZEIGE.

Bezeichnen Q Schnittpunkt von Linien PG und AB.

Verbinde die Punkte E und Q, F und G.

Trapez erhalten EFGQ wird der erforderliche Abschnitt sein.

https://pandia.ru/text/78/630/images/image004_91.gif" width="624" height="287">

2.4. Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch Punkte geht E, F, die auf den Kanten des Würfels und der Spitze liegen B.

Entscheidung. Konstruieren eines Abschnitts eines Würfels, der durch Punkte verläuft E, F und oben B,

Verbinden Sie die Punkte mit Segmenten E und B, F und b.

durch Punkte E und F Ziehe gerade Linien parallel bf und SEIN, bzw.

Das resultierende Parallelogramm BFGE wird der erforderliche Abschnitt sein.

2.5. Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch Punkte geht E, F, G an den Kanten des Würfels liegen.

Entscheidung. Konstruieren eines Abschnitts eines Würfels, der durch Punkte verläuft E, F, G,

Lassen Sie uns eine gerade Linie ziehen EF und bezeichnen P seinen Schnittpunkt mit ANZEIGE.

Bezeichnen Q,R Schnittpunkt einer Linie PG mit AB und Gleichstrom.

Bezeichnen S Schnittpunkt FR c SS 1.

Verbinde die Punkte E und Q, G und S.

Das resultierende Fünfeck EFSGQ wird der erforderliche Abschnitt sein.

2.6. Konstruieren Sie einen Abschnitt eines Würfels durch eine Ebene, die durch Punkte geht E, F, G an den Kanten des Würfels liegen.

Entscheidung. Konstruieren eines Abschnitts eines Würfels, der durch Punkte verläuft E, F, G,

Punkt finden P Schnittpunkt der Linie EF und Gesichtsebenen A B C D.

Bezeichnen Q, R Schnittpunkt einer Linie PG mit AB und CD.

Lassen Sie uns eine gerade Linie ziehen Rf und bezeichnen S, T seine Schnittpunkte mit CC 1 und DD 1.

Lassen Sie uns eine gerade Linie ziehen TE und bezeichnen U seinen Schnittpunkt mit EIN 1D 1.

Verbinde die Punkte E und Q, G und S, F und U.

Das resultierende Sechseck EUFSGQ wird der erforderliche Abschnitt sein.

2.7. Konstruieren Sie einen Abschnitt eines Tetraeders A B C D ANZEIGE und Durchlaufen der Punkte E, F.

Entscheidung. Verbinde die Punkte E und F. Durch den PunktF zeichne eine LinieFG, parallelANZEIGE.

Verbinde die Punkte G und E.

Das resultierende Dreieck EFG wird der erforderliche Abschnitt sein.

2.8. Konstruieren Sie einen Abschnitt eines Tetraeders A B C D eine Ebene parallel zum Rand CD und Durchlaufen der Punkte E, F .

Entscheidung. durch Punkte E und F Lassen Sie uns gerade zeichnen Z.B und FH, parallel CD.

Verbinde die Punkte G und F, E und H.

Das resultierende Dreieck EFG wird der erforderliche Abschnitt sein.

2.9. Konstruieren Sie einen Abschnitt eines Tetraeders A B C D Ebene, die durch die Punkte geht E, F, G.

Entscheidung. Konstruieren eines durch Punkte verlaufenden Abschnitts eines Tetraeders E, F, G,

Lassen Sie uns eine gerade Linie ziehen EF und bezeichnen P seinen Schnittpunkt mit BD.

Bezeichnen Q Schnittpunkt von Linien PG und CD.

Verbinde die Punkte F und Q, E und G.

Das resultierende Viereck EFQG wird der erforderliche Abschnitt sein.

IV. Zusammenfassung der Lektion.

v. Hausaufgaben S.14, S.27 Nr. 000 - Option 1, 2.