分母と整数が異なる分数の乗算。 分数と整数の掛け算と割り算のルール
通常の分数で実行できるもう 1 つの演算は乗算です。 問題を解くときにその基本的なルールを説明し、普通の分数にどのように乗算するかを示します。 自然数 3 つの普通の分数の掛け算を正しく行う方法など。
まず基本的なルールを書き留めましょう。
定義 1
1 つの普通の分数を掛けると、結果の分数の分子は元の分数の分子の積に等しく、分母はそれらの分母の積に等しくなります。 リテラル形式では、2 つの分数 a / b および c / d について、これは a b · c d = a · c b · d として表すことができます。
このルールを正しく適用する方法の例を見てみましょう。 一辺が 1 つの数値単位に等しい正方形があるとします。 すると図形の面積は1平方メートルになります。 ユニット。 この正方形を辺が 1 4 および 1 8 の数値単位に等しい等しい長方形に分割すると、32 個の長方形で構成されていることがわかります (8 4 = 32 であるため)。 したがって、それらのそれぞれの面積は、図全体の面積の1 32に等しくなります。 1 32平方メートル 単位。
5 8 数値単位と 3 4 数値単位に等しい辺を持つ影付きのフラグメントがあります。 したがって、その面積を計算するには、最初の分数に 2 番目の分数を掛ける必要があります。 5 8 · 3 4 平方に等しくなります。 単位。 しかし、フラグメントに含まれる長方形の数を単純に数えることができます。それらは 15 個あります。つまり、 総面積は 15 32 平方単位です。
5 3 = 15 および 8 4 = 32 なので、次の等式を書くことができます。
5 8 3 4 = 5 3 8 4 = 15 32
これは、普通の分数を乗算するために定式化した規則 (a b · c d = a · c b · d) を裏付けるものです。 これは、適正分数と仮分数の両方で同じように機能します。 異なる分母と同一の分母の両方をもつ分数の乗算に使用できます。
普通の分数の掛け算を含むいくつかの問題の解決策を見てみましょう。
例1
7 11 に 9 8 を掛けます。
解決
まず、7 と 9 を掛けて、指定された分数の分子の積を計算しましょう。 63 になりました。 次に、分母の積を計算すると、11 · 8 = 88 が得られます。 2 つの数字を合成すると、答えは 63 88 になります。
ソリューション全体は次のように記述できます。
7 11 9 8 = 7 9 11 8 = 63 88
答え: 7 11 · 9 8 = 63 88。
答えに約分が得られた場合は、計算を完了して約分を実行する必要があります。 不適切な分数が得られた場合は、そこから部分全体を分離する必要があります。
例 2
分数の積を計算する4 15および55 6.
解決
上で検討したルールによれば、分子と分子を乗算し、分母と分母を乗算する必要があります。 ソリューション レコードは次のようになります。
4 15 55 6 = 4 55 15 6 = 220 90
可約分数が得られました。 10で割り切れるもの。
分数を約してみましょう: 220 90 gcd (220, 90) = 10、220 90 = 220: 10 90: 10 = 22 9。 その結果、不適切な分数が得られ、そこから部分全体を選択して取得します。 帯分数: 22 9 = 2 4 9 .
答え: 4 15 55 6 = 2 4 9。
計算を容易にするために、乗算演算を実行する前に元の分数を減らすこともできます。そのためには、分数を a · c b · d の形式に減らす必要があります。 変数の値を単純な因子に分解し、同じものを減らしてみましょう。
特定のタスクのデータを使用して、これがどのようなものかを説明してみましょう。
例 3
積 4 15 55 6 を計算します。
解決
掛け算のルールに基づいた計算を書いてみましょう。 私たちは得るだろう:
4 15 55 6 = 4 55 15 6
4 = 2 2、55 = 5 11、15 = 3 5、6 = 2 3 なので、4 55 15 6 = 2 2 5 11 3 5 2 3 となります。
2 11 3 3 = 22 9 = 2 4 9
答え: 4 15 · 55 6 = 2 4 9 。
数値式通常の分数の乗算が行われるこの式には可換性の性質があります。つまり、必要に応じて因数の順序を変更できます。
a b · c d = c d · a b = a · c b · d
分数と自然数を掛ける方法
早速、基本的なルールを書き出して、実際に説明してみましょう。
定義 2
共通の分数に自然数を掛けるには、その分数の分子にその数値を掛ける必要があります。 この場合、最後の分数の分母は元の分数の分母と等しくなります。 公分数。 特定の分数 a b と自然数 n の乗算は、式 a b · n = a · n b として書くことができます。
任意の自然数は、分母が 1 に等しい通常の分数として表現できることを覚えておくと、この式を簡単に理解できます。
a b · n = a b · n 1 = a · n b · 1 = a · n b
具体的な例を挙げて私たちの考え方を説明しましょう。
例 4
積 2 の 27 掛ける 5 を計算します。
解決
元の分数の分子に 2 番目の係数を乗算した結果、10 が得られます。 上記のルールにより、結果として 10 27 が得られます。 ソリューション全体はこの投稿に記載されています。
2 27 5 = 2 5 27 = 10 27
答え: 2 27 5 = 10 27
自然数に分数を掛けるとき、結果を省略したり、帯分数として表したりする必要があることがよくあります。
例5
条件: 8 x 5 12 の積を計算します。
解決
上記のルールに従って、自然数に分子を掛けます。 その結果、5 12 8 = 5 8 12 = 40 12 が得られます。 最後の分数には 2 で割り切れる兆候があるため、これを約分する必要があります。
LCM (40, 12) = 4、つまり 40 12 = 40: 4 12: 4 = 10 3
あとは、部分全体を選択して、用意された答えを書き留めるだけです: 10 3 = 3 1 3。
このエントリでは、解全体: 5 12 8 = 5 8 12 = 40 12 = 10 3 = 3 1 3 を確認できます。
分子と分母を素因数分解して分数を減らすこともでき、結果はまったく同じになります。
答え: 5 12 8 = 3 1 3。
自然数に分数を乗算する数値式にも変位の特性があります。つまり、因数の順序は結果に影響しません。
a b · n = n · a b = a · n b
3 つ以上の公分数の掛け方
自然数の乗算に特徴的なのと同じ性質を、通常の分数の乗算の動作に拡張することができます。 これは、これらの概念の定義そのものから導かれます。
結合と可換性の知識のおかげで、3 つ以上の普通の分数を掛けることができます。 利便性を高めるために係数を再配置したり、数えやすいように括弧を配置したりすることは許容されます。
これがどのように行われるかを例で示してみましょう。
例6
4 つの公用分数 1 20、12 5、3 7、5 8 を掛けます。
解決策: まず、作業を記録しましょう。 1 20 · 12 5 · 3 7 · 5 8 となります。 すべての分子とすべての分母を掛け合わせる必要があります: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 。
掛け算を開始する前に、作業を少し楽にして、いくつかの数値を素因数に因数分解してさらに削減することができます。 これは、すでに準備されている結果のフラクションを減らすよりも簡単です。
1 12 3 5 20 5 7 8 = 1 (2 2 3) 3 5 2 2 5 5 7 (2 2 2) = 3 3 5 7 2 2 2 = 9,280
答え: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9,280。
例 7
5 つの数字 7 8 · 12 · 8 · 5 36 · 10 を掛けます。
解決
便宜上、分数 7 8 を数値 8 とグループ化し、数値 12 を分数 5 36 とグループ化することができます。これは、将来の略語が明らかになるためです。 結果として、以下が得られます。
7 8 12 8 5 36 10 = 7 8 8 12 5 36 10 = 7 8 8 12 5 36 10 = 7 1 2 2 3 5 2 2 3 3 10 = 7 5 3 10 = 7 5 10 3 = 350 3 = 116 2 3
答え: 7 8 12 8 5 36 10 = 116 2 3。
テキスト内のエラーに気付いた場合は、それを強調表示して Ctrl+Enter を押してください。
公用分数の掛け算
例を見てみましょう。
皿の上にリンゴの $\frac(1)(3)$ の部分があるとします。 その中の $\frac(1)(2)$ 部分を見つける必要があります。 必要な部分は、分数 $\frac(1)(3)$ と $\frac(1)(2)$ を乗算した結果です。 2 つの公分数を乗算した結果が公分数です。
2 つの普通の分数の掛け算
普通の分数の掛け算のルール:
分数と分数を乗算した結果は、分子が乗算される分数の分子の積に等しく、分母が分母の積に等しい分数になります。
例1
公用分数 $\frac(3)(7)$ と $\frac(5)(11)$ の乗算を実行します。
解決。
普通の分数を掛けるための規則を使用してみましょう。
\[\frac(3)(7)\cdot \frac(5)(11)=\frac(3\cdot 5)(7\cdot 11)=\frac(15)(77)\]
答え:$\frac(15)(77)$
分数を乗算すると、約分できる分数または不適切な分数が得られる場合は、それを簡略化する必要があります。
例 2
分数 $\frac(3)(8)$ と $\frac(1)(9)$ を掛けます。
解決。
通常の分数の乗算には次の規則を使用します。
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)\]
その結果、約分可能な分数が得られました ($3$ による除算に基づいています。分数の分子と分母を $3$ で割ると、次のようになります:
\[\frac(3)(72)=\frac(3:3)(72:3)=\frac(1)(24)\]
簡単な解決策:
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)=\frac(1) (24)\]
答え:$\frac(1)(24).$
分数を掛けるときは、積が見つかるまで分子と分母を減らすことができます。 この場合、分数の分子と分母を単純な因数に分解し、その後、繰り返しの因数をキャンセルして結果を求めます。
例 3
分数 $\frac(6)(75)$ と $\frac(15)(24)$ の積を計算します。
解決。
普通の分数を掛けるための公式を使用してみましょう。
\[\frac(6)(75)\cdot \frac(15)(24)=\frac(6\cdot 15)(75\cdot 24)\]
明らかに、分子と分母には、ペアで $2$、$3$、$5$ という数値に短縮できる数値が含まれています。 分子と分母を単純な因数に因数分解して、約分してみましょう。
\[\frac(6\cdot 15)(75\cdot 24)=\frac(2\cdot 3\cdot 3\cdot 5)(3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3)=\frac(1)(5\cdot 2\cdot 2)=\frac(1)(20)\]
答え:$\frac(1)(20).$
分数を乗算するときは、交換法則を適用できます。
公分数と自然数の掛け算
公分数と自然数の乗算規則は次のとおりです。
分数に自然数を乗算した結果は、分子が乗算された分数の分子と自然数の積に等しく、分母が乗算された分数の分母に等しい分数になります。
ここで、$\frac(a)(b)$ は普通の分数、$n$ は自然数です。
例 4
分数 $\frac(3)(17)$ に $4$ を掛けます。
解決。
普通の分数と自然数を掛けるための規則を使用してみましょう。
\[\frac(3)(17)\cdot 4=\frac(3\cdot 4)(17)=\frac(12)(17)\]
答え:$\frac(12)(17).$
分数の約分または仮分数による乗算の結果を確認することを忘れないでください。
例5
分数 $\frac(7)(15)$ に数値 $3$ を掛けます。
解決。
分数に自然数を掛ける公式を使ってみましょう。
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)\]
数値 $3$) で割ることにより、結果の端数を減らすことができることがわかります。
\[\frac(21)(15)=\frac(21:3)(15:3)=\frac(7)(5)\]
結果は不正確な分数でした。 部分全体を選択してみましょう。
\[\frac(7)(5)=1\frac(2)(5)\]
簡単な解決策:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)=\frac(7)(5)=1\frac(2) (5)\]
分数は、分子と分母の数値を素因数分解で置き換えることによっても減らすことができます。 この場合、解決策は次のように記述できます。
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(7\cdot 3)(3\cdot 5)=\frac(7)(5)= 1\frac(2)(5)\]
答え:$1\frac(2)(5).$
分数に自然数を掛けるときは、交換法則を使用できます。
分数の割り算
除算演算は乗算の逆であり、その結果は分数になります。これを得るには、既知の分数を掛ける必要があります。 有名な作品 2つの分数。
2 つの普通の分数の割り算
普通の分数の割り算のルール:明らかに、結果の分数の分子と分母は因数分解して約分できます。
\[\frac(8\cdot 35)(15\cdot 12)=\frac(2\cdot 2\cdot 2\cdot 5\cdot 7)(3\cdot 5\cdot 2\cdot 2\cdot 3)= \frac(2\cdot 7)(3\cdot 3)=\frac(14)(9)\]
その結果、不適切な分数が得られ、そこから部分全体を選択します。
\[\frac(14)(9)=1\frac(5)(9)\]
答え:$1\frac(5)(9).$
分数と分数、または分数と数値を正しく乗算するには、次のことを知っておく必要があります。 簡単なルール。 次に、これらのルールを詳細に分析します。
普通の分数と分数を掛けます。
分数と分数を掛けるには、これらの分数の分子の積と分母の積を計算する必要があります。
\(\bf \frac(a)(b) \times \frac(c)(d) = \frac(a \times c)(b \times d)\\\)
例を見てみましょう:
最初の分数の分子と 2 番目の分数の分子を掛け、また、最初の分数の分母と 2 番目の分数の分母を掛けます。
\(\frac(6)(7) \times \frac(2)(3) = \frac(6 \times 2)(7 \times 3) = \frac(12)(21) = \frac(4 \ 3 倍)(7 \times 3) = \frac(4)(7)\\\)
小数 \(\frac(12)(21) = \frac(4 \times 3)(7 \times 3) = \frac(4)(7)\\\) は 3 減りました。
分数に数値を掛けます。
まずはルールを覚えましょう 任意の数値は分数 \(\bf n = \frac(n)(1)\) として表すことができます。
乗算するときはこのルールを使用しましょう。
\(5 \times \frac(4)(7) = \frac(5)(1) \times \frac(4)(7) = \frac(5 \times 4)(1 \times 7) = \frac (20)(7) = 2\frac(6)(7)\\\)
仮分数 \(\frac(20)(7) = \frac(14 + 6)(7) = \frac(14)(7) + \frac(6)(7) = 2 + \frac(6)( 7)= 2\frac(6)(7)\\\) に変換 混合分数.
言い換えると、 数値に分数を掛けるときは、数値に分子を掛け、分母は変更しません。例:
\(\frac(2)(5) \times 3 = \frac(2 \times 3)(5) = \frac(6)(5) = 1\frac(1)(5)\\\\\) \(\bf \frac(a)(b) \times c = \frac(a \times c)(b)\\\)
帯分数の掛け算。
帯分数を乗算するには、まず各帯分数を仮分数として表し、次に乗算規則を使用する必要があります。 分子と分子を掛け、分母と分母を掛けます。
例:
\(2\frac(1)(4) \times 3\frac(5)(6) = \frac(9)(4) \times \frac(23)(6) = \frac(9 \times 23) (4 \times 6) = \frac(3 \times \color(red) (3) \times 23)(4 \times 2 \times \color(red) (3)) = \frac(69)(8) = 8\frac(5)(8)\\\)
逆数の分数と数値の乗算。
分数 \(\bf \frac(a)(b)\) は、a≠0,b≠0 の場合、分数 \(\bf \frac(b)(a)\) の逆数です。
分数 \(\bf \frac(a)(b)\) と \(\bf \frac(b)(a)\) は逆分数と呼ばれます。 逆数の積は 1 に等しくなります。
\(\bf \frac(a)(b) \times \frac(b)(a) = 1 \\\)
例:
\(\frac(5)(9) \times \frac(9)(5) = \frac(45)(45) = 1\\\)
関連する質問:
分数と分数を掛けるにはどうすればよいですか?
答え: 普通の分数の積は、分子と分子、分母と分母の掛け算です。 帯分数の積を求めるには、仮分数に変換し、規則に従って乗算する必要があります。
分数を掛ける方法 分母が異なる?
答え: 分数の分母が同じか異なるかは問題ではありません。掛け算は、分子と分子、分母と分母の積を求めるルールに従って行われます。
帯分数のかけ算はどうやって行うのですか?
答え: まず、帯分数を仮分数に変換し、次に乗算の規則を使用して積を求める必要があります。
数値に分数を掛けるにはどうすればよいですか?
答え: 数値に分子を掛けますが、分母はそのままにします。
例 #1:
積を計算します。 a) \(\frac(8)(9) \times \frac(7)(11)\) b) \(\frac(2)(15) \times \frac(10)(13) \)
解決:
a) \(\frac(8)(9) \times \frac(7)(11) = \frac(8 \times 7)(9 \times 11) = \frac(56)(99)\\\\ \)
b) \(\frac(2)(15) \times \frac(10)(13) = \frac(2 \times 10)(15 \times 13) = \frac(2 \times 2 \times \color(赤) (5))(3 \times \color(red) (5) \times 13) = \frac(4)(39)\)
例2:
数値と分数の積を計算します。 a) \(3 \times \frac(17)(23)\) b) \(\frac(2)(3) \times 11\)
解決:
a) \(3 \times \frac(17)(23) = \frac(3)(1) \times \frac(17)(23) = \frac(3 \times 17)(1 \times 23) = \frac(51)(23) = 2\frac(5)(23)\\\\\)
b) \(\frac(2)(3) \times 11 = \frac(2)(3) \times \frac(11)(1) = \frac(2 \times 11)(3 \times 1) = \frac(22)(3) = 7\frac(1)(3)\)
例 #3:
分数 \(\frac(1)(3)\) の逆数を書きますか?
答え: \(\frac(3)(1) = 3\)
例 #4:
2 つの相互に逆数の分数の積を計算します。 a) \(\frac(104)(215) \times \frac(215)(104)\)
解決:
a) \(\frac(104)(215) \times \frac(215)(104) = 1\)
例5:
逆分数は次のようになります。
a) 適切な分数と同時に。
b) 同時に仮分数。
c) 同時に自然数か?
解決:
a) 最初の質問に答えるために、例を挙げてみましょう。 分数 \(\frac(2)(3)\) は適切で、その逆分数は \(\frac(3)(2)\) に等しくなります。これは仮分数です。 答え: いいえ。
b) 分数のほとんどすべての列挙ではこの条件は満たされませんが、同時に仮分数であるという条件を満たす数がいくつかあります。 たとえば、仮分数は \(\frac(3)(3)\) で、その逆分数は \(\frac(3)(3)\) に等しくなります。 2 つの仮分数が得られます。 回答: 特定の条件下では、分子と分母が等しいとは限りません。
c) 自然数とは、たとえば、1、2、3、…など、数を数えるときに使用する数です。 数値 \(3 = \frac(3)(1)\) をとった場合、その逆分数は \(\frac(1)(3)\) になります。 分数 \(\frac(1)(3)\) は自然数ではありません。 すべての数値を調べた場合、その数値の逆数は 1 を除いて常に分数になります。数値 1 を取ると、その逆数は \(\frac(1)(1) = \frac(1) になります。 )(1) = 1\)。 数字 1 は自然数です。 答え: これらは 1 つの場合にのみ、同時に自然数になることができます。これが数値 1 である場合です。
例6:
帯分数の積を計算します。 a) \(4 \times 2\frac(4)(5)\) b) \(1\frac(1)(4) \times 3\frac(2)(7)\ )
解決:
a) \(4 \times 2\frac(4)(5) = \frac(4)(1) \times \frac(14)(5) = \frac(56)(5) = 11\frac(1) )(5)\\\\ \)
b) \(1\frac(1)(4) \times 3\frac(2)(7) = \frac(5)(4) \times \frac(23)(7) = \frac(115)( 28) = 4\frac(3)(7)\)
例7:
2 つの逆数を同時に帯分数にすることはできますか?
例を見てみましょう。 帯分数 \(1\frac(1)(2)\) を考えて、その逆分数を見つけてみましょう。これを行うには、それを仮分数 \(1\frac(1)(2) = \frac(3) に変換します。 )(2) \) 。 その逆分数は \(\frac(2)(3)\) に等しくなります。 分数 \(\frac(2)(3)\) は固有の分数です。 答え: 相互に反転した 2 つの分数を同時に帯分数にすることはできません。
もう熊手を乗り越えてください! 🙂
分数の掛け算と割り算。
注意!
追加もあります
特別セクション 555 の資料。
とても「あまり」ではない人のために。 »
そして、「とてもそう」という人たちにとっても。 ")
この演算は足し算や引き算よりもずっと楽しいです。 そのほうが簡単だからです。 分数と分数を掛けるには、分子 (これが結果の分子になります) と分母 (これが分母になります) を掛ける必要があることに注意してください。 あれは:


すべてが非常にシンプルです。 そして、共通点を探さないでください。 ここには彼は必要ありません...
分数を分数で割るには、逆算する必要があります。 2番(これは重要です!) 分数と乗算を行います。つまり、次のようになります。


整数や分数の掛け算や割り算が出てきても大丈夫です。 足し算と同じように、分母に 1 を入れた整数から分数を作ります。 例えば:

高校では、3 階建て (または 4 階建て!) の分数を扱わなければならないことがよくあります。 例えば:
この部分をまともに見せるにはどうすればよいでしょうか? はい、とてもシンプルです! 2 点除算を使用します。

ただし、分割の順序を忘れないでください。 掛け算とは異なり、ここでは非常に重要です。 もちろん、4:2 と 2:4 を混同することはありません。 しかし、3 階建ての部分では間違いを犯しやすいです。 たとえば次の点に注意してください。
最初のケース (左側の式):

2 番目の式 (右側の式):

違いを感じますか? 4と1/9!
分割の順序は何によって決まりますか? 括弧を使用するか、(ここのように) 水平線の長さを使用します。 目を養いましょう。 括弧やダッシュがない場合は、次のようになります。
次に、割り算と掛け算をします 左から右の順に!
そしてもう1つの非常にシンプルで重要なテクニック。 度を伴うアクションでは、それは非常に役立ちます。 1 を任意の分数、たとえば 13/15 で割ってみましょう。

ショットがひっくり返った! そして、これは常に起こります。 1 を任意の分数で割ると、結果は同じ分数になりますが、上下が逆になるだけです。
分数を使った演算は以上です。 事は非常に単純ですが、十分すぎるほどのエラーが発生します。 実践的なアドバイスを考慮に入れると、間違い(間違い)が少なくなります。
1. 分数式を扱うときに最も重要なことは、正確さと注意力です。 これらは一般的な言葉ではなく、良い願いでもありません。 これは切実な必需品です! 統一国家試験のすべての計算は、集中的かつ明確な本格的なタスクとして実行してください。 暗算でめちゃくちゃになるよりは、下書きに 2 行余分に書いたほうが良いでしょう。
2. の例では 他の種類分数 - 通常の分数に進みます。
3. すべての分数を止まるまで減らします。
4. 2 点による除算を使用して、複数レベルの分数式を通常の分数式に還元します (割り算の順序に従います)。
必ず完了しなければならないタスクは次のとおりです。 答えはすべてのタスクの後に与えられます。 このトピックと実践的なヒントに関する資料を使用してください。 正しく解くことができた例題の数を見積もってください。 初めて! 電卓なしでも! そして正しい結論を導き出します。
覚えておいてください - 正しい答えは 2回目(特に3回目)以降に受け取ったものはカウントされません!それが過酷な人生なのです。
それで、 試験モードで解く ! ちなみに、これはすでに統一国家試験の準備です。 例題を解いて確認し、次の問題を解きます。 私たちはすべてを決定しました - 最初から最後まで再度確認しました。 だけ それから答えを見てください。


あなたに合った回答を探しています。 いわば、誘惑から遠ざけて、意図的にそれらを混乱させて書き留めました。 ここに、セミコロンで区切られた答えが表示されます。
0; 17/22; 3/4; 2/5; 1; 25.
さて、結論を導き出します。 すべてがうまくいったなら、私はあなたにとって幸せです! 分数を使った基本的な計算は問題ありません。 もっと本格的なこともできますよ。 そうでなければ。
したがって、2 つの問題のうちの 1 つが発生します。 またはその両方を同時に。)知識の欠如と(または)不注意。 しかし。 これ 解決可能な 問題。
これらすべて (そしてさらに!) の例は、特別セクション 555「分数」で説明されています。 何を、なぜ、どのようにするのかについての詳細な説明付き。 この分析は、知識やスキルが不足している場合に非常に役立ちます。
はい、そして 2 番目の問題には何かあります。) 実践的なアドバイス, もっと注意深くなる方法。 はいはい! 応用できるアドバイス 毎.
知識と注意力に加えて、成功にはある程度の自動性が必要です。 どこで入手できますか? 重いため息が聞こえます...はい、練習中のみで、他の場所ではありません。
トレーニングのために Web サイト 321start.ru にアクセスできます。 「試してみる」オプションには、誰でも使える 10 個の例があります。 即時認証付き。 登録ユーザー向け - 簡単な例から深刻な例まで 34 例。 これは端数でのみ発生します。
このサイトが気に入ったら。
ちなみに、他にも興味深いサイトがいくつかあります。)
ここでは例題を解く練習をし、自分のレベルを知ることができます。 即時検証によるテスト。 興味を持って学びましょう!)
ここでは関数と導関数について知ることができます。
ルール1。
分数に自然数を掛けるには、その分子にこの数値を掛け、分母を変更しないようにする必要があります。
ルール2。
分数と分数を乗算するには:
1. これらの分数の分子の積と分母の積を求めます。
2. 最初の積を分子として、2 番目の積を分母として書きます。
ルール3。
帯分数を掛けるには、帯分数を仮分数として書き、分数のかけ算のルールを使用する必要があります。
ルール4。
ある分数を別の分数で割るには、被除数に除数の逆数を掛ける必要があります。
例1.
計算する

例2。
計算する
![]()
例 3.
計算する
例4.
計算する
数学。 その他の素材
数値の有理累乗。 (
数値を自然累乗します。 (
代数不等式を解くための一般化区間法 (著者 A.V. Kolchanov)
代数不等式を解くときに因数を置き換える方法 (著者 Kolchanov A.V.)
分裂の兆し (ルング・アレナ)
「普通の分数の掛け算と割り算」というテーマで自分自身をテストしてみましょう
分数の掛け算
いくつかの可能なオプションで普通の分数の乗算を検討します。
公用分数と分数の掛け算
これは、以下を使用する必要がある最も単純なケースです。 分数のかけ算のルール.
に 分数と分数を掛ける、 必要:
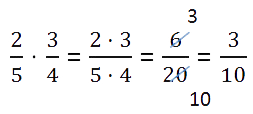
分子と分母を掛ける前に、分数が約分できるかどうかを確認してください。 計算で分数を減らすと、計算がはるかに簡単になります。

分数と自然数の掛け算
分数を作るには 自然数を掛ける分数の分子にこの数値を掛け、分数の分母は変更しないでおく必要があります。
乗算の結果が仮分数の場合は、帯分数に変換すること、つまり全体を強調表示することを忘れないでください。

帯分数の乗算
帯分数を掛けるには、まず仮分数に変換してから、普通の分数の掛け算のルールに従って掛け算を行う必要があります。

分数に自然数を掛ける別の方法
計算を行う場合、公分数に数値を掛ける別の方法を使用した方が便利な場合があります。
分数に自然数を掛けるには、分数の分母をこの数値で割り、分子を同じにする必要があります。

例からわかるように、このバージョンのルールは、分数の分母が余りのない自然数で割り切れる場合に使用するのがより便利です。
分数を数値で割る
分数を数値で割る最も速い方法は何ですか? 理論を分析し、結論を導き出し、例を使用して、新しい短い規則を使用して分数を数値で割る方法を見てみましょう。
通常、分数を数値で割る場合は、分数の割り算の規則に従います。 最初の数値 (分数) に 2 番目の数値の逆数を掛けます。 2 番目の数値は整数なので、その逆数は分子が次のような分数になります。 1に等しい、分母は指定された数値です。 分数を自然数で割ると、概略的には次のようになります。
![]()
このことから、次のように結論付けられます。
分数を数値で割るには、分母にその数値を掛け、分子はそのままにする必要があります。 ルールはさらに簡潔に定式化できます。
分数を数値で割る場合、その数値は分母に入ります。
分数を数値で割る:

分数を数値で割るには、分子を変更せずに書き直し、分母にこの数値を掛けます。 6と3を3ずつ減らします。

分数を数値で割るときは、分子を書き換えて分母にその数値を掛けます。 16 と 24 を 8 で減らします。

分数を数値で割る場合、その数値は分母に入りますので、分子はそのままにして、分母に約数を掛けます。 21 と 35 を 7 で減らします。
分数の掛け算と割り算
前回は、分数の足し算と引き算の方法を学習しました (レッスン「分数の足し算と引き算」を参照)。 これらのアクションの最も困難な部分は、分数を共通の分母にすることでした。
今度は掛け算と割り算を扱います。 幸いなことに、これらの演算は加算や減算よりもさらに単純です。 まず、整数部分が分離されていない 2 つの正の分数がある、という最も単純なケースを考えてみましょう。
2 つの分数を乗算するには、それらの分子と分母を別々に乗算する必要があります。 最初の数値が新しい分数の分子となり、2 番目の数値が分母になります。
2 つの分数を除算するには、最初の分数に「反転した」2 番目の分数を掛ける必要があります。
定義から、分数の除算は乗算に帰着することがわかります。 分数を「反転」するには、分子と分母を入れ替えるだけです。 したがって、このレッスンでは主に掛け算を考えていきます。
乗算の結果、約分数が発生する可能性があります (実際に発生することもよくあります)。もちろん、これは約分する必要があります。 すべての縮小の結果、分数が正しくないことが判明した場合は、部分全体を強調表示する必要があります。 しかし、乗算で絶対に起こらないのは、共通の分母への還元です。つまり、交差法はなく、最大因数と最小公倍数です。
タスク。 式の意味を調べます。
定義により、次のようになります。

分数と整数部および負の分数の乗算
分数に整数部分が含まれている場合は、それらを不適切な分数に変換してから、上で概説したスキームに従って乗算する必要があります。
分数の分子、分母、またはその前にマイナスがある場合、次の規則に従って、そのマイナスを乗算から除外したり、完全に削除したりできます。
- プラスとマイナスはマイナスになります。
- 2 つの否定が肯定になります。
- ネガが完全に消えるまで、ペアでネガを取り消します。 極端な場合には、1 つのマイナス、つまり相手がいなかったマイナスが生き残る可能性があります。
- マイナスが残っていない場合、操作は完了です。乗算を開始できます。 最後のマイナスに対応するペアがなかったために取り消し線が引かれていない場合は、それを乗算の範囲外とします。 結果は負の分数になります。
これまで、これらのルールは、負の分数を加算および減算する場合、つまり部分全体を削除する必要がある場合にのみ適用されていました。 作品の場合、いくつかの欠点を一度に「燃やす」ために一般化できます。
すべての分数を不適切な分数に変換し、乗算からマイナスを取り除きます。 残ったものを掛け合わせます 通常のルール。 我々が得る:

整数部分が強調表示されている分数の前に表示されるマイナスは、整数部分だけを指すのではなく、分数全体を具体的に指すことをもう一度思い出してください (これは最後の 2 つの例に当てはまります)。
こちらも注意 負の数:乗算する場合は括弧で囲みます。 これは、乗算記号からマイナスを分離し、表記全体をより正確にするために行われます。
その場で分数を減らす
乗算は非常に労力を要する演算です。 ここでの数値は非常に大きいことが判明したため、問題を単純化するために、さらに端数を減らしてみることができます。 乗算の前に。 実際、本質的には、分数の分子と分母は通常の因数であるため、分数の基本的な性質を使用して約分できます。 例を見てみましょう。
![]()

すべての例で、削減された数とその残りの数は赤色でマークされています。
注意してください: 最初のケースでは、乗数は完全に減少しました。 その代わりに、一般的に書く必要のない単位が残ります。 2 番目の例では、完全な削減は達成できませんでしたが、それでも総計算量は減少しました。
ただし、分数の足し算や引き算の際には、このテクニックを決して使用しないでください。 はい、同様の数値を削減したい場合があります。 ここで見てください:
そんなことはできません!
このエラーは、加算するときに分数の分子が数値の積ではなく和を生成するために発生します。 したがって、分数の主プロパティを適用することは不可能です。 私たちが話しているのは特に数値の掛け算について。
端数を減らす理由は他にありません。 正しい解決策前のタスクは次のようになります。
ご覧のとおり、正解はそれほど美しくないことが判明しました。 一般に、注意してください。
分数の割り算。
分数を自然数で割る。
分数を自然数で割る例
自然数を分数で割ります。
自然数を分数で割る例
普通の分数の割り算。
普通の分数の割り算の例
帯分数の割り算。
- ある帯分数を別の帯分数で割るには、次の操作を行う必要があります。
- 混合分数を仮分数に変換します。
- 最初の分数に 2 番目の分数の逆数を掛けます。
- 得られた分数を減らします。
- 仮分数が出た場合は、その仮分数を帯分数に変換します。
- 混合分数を仮分数に変換します。
- 分数の分子と分母を掛ける。
- 端数を減らす。
- 仮分数が得られた場合は、仮分数を帯分数に変換します。
- アンダーアンドアンダー - 再加工された曲「Spring Tango」(時が来る - 鳥が南から飛ぶ) - 音楽。 ヴァレリー・ミリャエフ 十分に聞いていなかった、理解できなかった、理解できなかった、推測できなかったという意味で、私はすべての動詞を切り離せないもので書きました、接頭辞ネドについて知りませんでした。 それは起こります、[…]
- ページが見つかりません 3 回目の最終読会では、特別行政区 (SAR) の創設を規定する政府文書のパッケージが採択されました。 欧州連合を離脱した結果、英国は欧州 VAT 地域に含まれなくなり、[…]
- 合同捜査委員会は秋に開催される 合同調査委員会は秋に開催される予定 全ての法執行機関による捜査は、4回目の試みで一つ屋根の下で行われる予定 イズベスチヤ通信によると、すでに2014年の秋にウラジミール・プーチン大統領[ …]
- アルゴリズムの特許 アルゴリズムの特許とはどのようなもの アルゴリズムの特許はどのように作成されるのか 準備 技術的な説明特に特許取得を目的とした信号やデータの保存、処理、送信方法には、通常、特別な困難は存在しません。また、[…]
- 年金に関する新しい法案について知っておくべき重要なこと 1993 年 12 月 12 日のロシア連邦憲法 (2008 年 12 月 30 日付のロシア連邦憲法の改正に関してロシア連邦法によって行われた改正を考慮する) N 6- FKZ、2008 年 12 月 30 日付 N 7-FKZ、[…]
- 女性の年金についての面白い小ネタがその日のヒーローに、男性がその日のヒーローに、男性はその日のヒーローに合唱、女性は年金受給者への献身、女性、面白い。年金受給者のためのコンテストは興味深いだろう。プレゼンター: 親愛なる友人! ちょっとまってください! 感覚! のみ […]
帯分数の割り算の例
1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16
2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7
わいせつなコメントは削除され、投稿者はブラックリストに登録されます。
OnlineMSchool へようこそ.
私の名前はドヴジク・ミハイル・ヴィクトロヴィッチです。 私はこのサイトの所有者兼著者であり、すべての理論資料を書き、開発も行いました。 オンライン演習数学の勉強に使える電卓も。
分数。 分数の掛け算と割り算。
普通の分数と分数を掛けます。
普通の分数を掛けるには、分子と分子を掛け (積の分子を取得します)、分母と分母を掛けます (積の分母を取得します)。
分数の乗算の公式:


分子と分母の乗算を開始する前に、分数が約分できるかどうかを確認する必要があります。 端数を減らすことができれば、その後の計算が容易になります。
注記! ここで共通点を探す必要はありません!!
公用分数を分数で割ります。
普通の分数を分数で割るのは次のように行われます。2 番目の分数を裏返し (つまり、分子と分母を変更し)、その後、分数が掛けられます。
普通の分数を割る公式:


分数に自然数を掛けます。
注記!分数に自然数を掛ける場合、分数の分子には自然数が掛けられ、分数の分母は変わりません。 積の結果が仮分数である場合は、必ずその部分全体を強調表示して、仮分数を帯分数に変えてください。

自然数を含む分数の割り算。
見た目ほど怖くないです。 足し算と同様に、整数を分母に 1 を含む分数に変換します。 例えば:

帯分数の掛け算。
分数の掛け算のルール (混合):
注記!帯分数と別の帯分数を掛けるには、まず仮分数の形に変換してから、普通の分数の掛け算の規則に従って掛けます。

分数に自然数を掛ける 2 番目の方法。
公分数に数値を掛ける 2 番目の方法を使用する方が便利な場合があります。
注記!分数に自然数を掛けるには、分数の分母をこの数値で割り、分子を変更しない必要があります。

上記の例から、分数の分母を剰余なしで自然数で割る場合に、このオプションを使用すると便利であることが明らかです。
多層階部分。
高校では、3 階建て (またはそれ以上) の分数がよく出てきます。 例:
このような分数を通常の形式に戻すには、2 点による除算を使用します。

注記!分数を割り算するとき、割り算の順序は非常に重要です。 ここで混乱しやすいので注意してください。
注記、 例えば:
1 を任意の分数で割った場合、結果は同じ分数を反転しただけになります。
分数の掛け算と割り算に関する実践的なヒント:
1. 分数式を扱うときに最も重要なことは、正確さと注意力です。 すべての計算を慎重かつ正確に、集中して明確に実行します。 暗算で迷うよりは、下書きに数行余分に書いたほうが良いでしょう。
2. さまざまなタイプの分数を使用するタスクでは、通常の分数のタイプに進みます。
3. すべての分数を、約分できなくなるまで約分します。
4. 多段階の分数式を 2 点による除算を使用して通常の分数式に変換します。
) と分母ごとに計算します (積の分母が得られます)。
分数の乗算の公式:
例えば:

分子と分母の乗算を開始する前に、分数が約分できるかどうかを確認する必要があります。 端数を減らすことができれば、その後の計算が容易になります。
公用分数を分数で割ります。

自然数を含む分数の割り算。
見た目ほど怖くないです。 加算の場合と同様に、整数を分母に 1 を含む分数に変換します。 例えば:

帯分数の掛け算。
分数の掛け算のルール (混合):
- 混合分数を仮分数に変換します。
- 分数の分子と分母を掛ける。
- 端数を減らす。
- 仮分数が得られた場合は、仮分数を帯分数に変換します。
注記!帯分数と別の帯分数を掛けるには、まず仮分数の形に変換してから、普通の分数の掛け算の規則に従って掛けます。

分数に自然数を掛ける 2 番目の方法。
公分数に数値を掛ける 2 番目の方法を使用する方が便利な場合があります。
注記!分数に自然数を掛けるには、分数の分母をこの数値で割り、分子を変更しない必要があります。

上記の例から、分数の分母を剰余なしで自然数で割る場合に、このオプションを使用すると便利であることが明らかです。
多層階部分。
高校では、3 階建て (またはそれ以上) の分数がよく出てきます。 例:
このような分数を通常の形式に戻すには、2 点による除算を使用します。

注記!分数を割り算するとき、割り算の順序は非常に重要です。 ここで混乱しやすいので注意してください。
注記、 例えば:
1 を任意の分数で割った場合、結果は同じ分数を反転しただけになります。
分数の掛け算と割り算に関する実践的なヒント:
1. 分数式を扱うときに最も重要なことは、正確さと注意力です。 すべての計算を慎重かつ正確に、集中して明確に実行します。 暗算で迷うよりは、下書きに数行余分に書いたほうが良いでしょう。
2. さまざまなタイプの分数を使用するタスクでは、通常の分数のタイプに進みます。
3. すべての分数を、約分できなくなるまで約分します。
4. 多段階の分数式を 2 点による除算を使用して通常の分数式に変換します。
5. 頭の中で単位を分数で割ります。分数をひっくり返すだけです。

 入り口
入り口