底が異なり、指数が同じ対数。 対数の公式。 対数の例の解決策。 10 進数と自然対数

対数の定義

a を底とする b の対数は、b を得るために a を累乗する必要がある指数です。

番号e数学では、式が達成しようとする限界を示すのが通例です

番号eは 無理数- 1 と比較できない数。整数でも分数でも正確に表現できません。 合理的な番号。

手紙 e- ラテン語の最初の文字 解明する- 誇示するため、数学でこの名前が付けられました 指数関数的- 指数関数。

番号 e数学や、何らかの形でニーズに合わせて数学的計算を使用するすべての科学で広く使用されています。

対数。 対数の性質

定義: 対数 正数基数 b は、数値 b を得るために数値 a を累乗する必要がある c の指数です。

基本的な対数恒等式:

7) 新しい拠点に移動するための公式:

lna = log e a, e ≈ 2.718…

「対数」というトピックに関する問題とテスト。 対数の性質」

• 対数 - 数学における統一国家試験を復習するための重要なトピック

このトピックのタスクを正常に完了するには、対数の定義、対数の性質、基本的な対数恒等式、10 進数と自然対数の定義を理解しておく必要があります。 このトピックに関する問題の主な種類は、対数式の計算と変換を伴う問題です。 次の例を使用して、その解決策を考えてみましょう。

解決：対数の性質を使用すると、次のようになります。

解決：度の特性を使用すると、次のようになります。

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

対数、公式、証明の性質。

対数には次の数があります 特徴的な性質。 この記事では主なものについて見ていきます 対数の性質。 ここでは、それらの公式を示し、対数の性質を公式の形式で書き留め、その応用例を示し、対数の性質の証明も示します。

ページナビゲーション。

対数、公式の基本的な性質

覚えやすく使いやすいように、次のように想像してみましょう。 対数の基本的な性質数式のリストの形式で。 次の段落では、その定式化、証拠、使用例、および必要な説明を示します。

単位の対数の性質: a>0、a≠1 の場合、log a 1=0。

底に等しい数値の対数: log a a=1 (a>0、a≠1)。

底のべき乗の対数の特性: log a a p =p、ここで、a>0、a≠1、p は任意の実数です。

2 つの正の数の積の対数: log a (x y)=log a x+log a y 、 a>0 、 a≠1 、 x>0 、 y>0 、
n 個の正の数の積の対数の性質: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n 、 a>0 、 a≠1 、 x 1 >0、x 2 >0、…、x n >0 。

商の対数の性質: ここで、a>0、a≠1、x>0、y>0。

数値の累乗の対数: log a b p =p・log a |b| ここで、a>0、a≠1、b および p は、次数 b p が意味を持ち、b p >0 となるような数値です。

結果： 、ここで、a>0、a≠1、n – 自然数、1より大きい、b>0。

帰結 1: 、 a>0 、 a≠1 、 b>0 、 b≠1 。

推論 2: 、 a>0 、 a≠1 、 b>0 、 p と q は実数、 q≠0 、特に b=a の場合、次のようになります。 .

配合と特性の証明

対数の書かれた性質の定式化と証明に進みます。 対数のすべての特性は、対数の定義とそこから派生する基本的な対数恒等式、および次数の特性に基づいて証明されます。

まずは始めましょう 1の対数の性質。 その定式化は次のとおりです: 1 の対数 ゼロに等しい、 あれは、 ログ 1=0 a>0 の場合、a≠1。 証明は難しくありません。上記の条件 a>0 および a≠1 を満たす任意の a に対して a 0 =1 であるため、証明される等価 log a 1=0 は対数の定義から直接得られます。

考慮したプロパティの適用例を示します。log 3 1=0、log1=0、および です。

次のプロパティに進みましょう。 底に等しい数の対数 1に等しい 、 あれは、 ログ a a=1 a>0 の場合、a≠1。 実際、任意の a に対して a 1 =a なので、対数 log a a=1 の定義によります。

この対数の性質を使用する例としては、等式 log 5 5=1、log 5.6 5.6、lne=1 などがあります。

対数の底に等しい数のべき乗の対数は指数に等しい。 対数のこの特性は、次の形式の式に対応します。 log a a p =pここで、a>0、a≠1、および p – 任意の実数。 この特性は、対数の定義から直接得られます。 対数記号の下の数値を底のべき乗として表すことができる場合、対数の値をすぐに示すことができることに注意してください。これについては、対数の計算の記事で詳しく説明します。

たとえば、log 2 2 7 =7、log10 -4 =-4、および .

2 つの正の数の積の対数 x と y は、次の数値の対数の積に等しくなります。 log a (x y)=log a x+log a y、a>0、a≠1。 積の対数の性質を証明してみましょう。 次数の性質により、 a log a x + log a y =a log a x ·a log a y となり、主対数恒等式により a log a x =x および a log a y =y となるため、a log a x ·a log a y となります。 =x・y。 したがって、log a x+log a y =x・yとなり、対数の定義により、等しいことが証明されます。

積の対数のプロパティを使用する例を示します: log 5 (2 3)=log 5 2+log 5 3 および .

積の対数の特性は、次のように、有限数 n の正の数 x 1 、 x 2 、…、 x n の積に一般化できます。 log a (x 1 · x 2 ·… · x n)= log a x 1 +log a x 2 +…+log a x n。 この等価性は、数学的帰納法を使用して問題なく証明できます。

たとえば、積の自然対数は、数値 4、e、および の 3 つの自然対数の合計で置き換えることができます。

2 つの正の数の商の対数 x と y は、これらの数値の対数間の差に等しくなります。 商の対数の性質は、次の形式の式に対応します。 ここで、a>0、a≠1、x および y は正の数です。 この公式の妥当性は、積の対数の公式と同様に証明されています。 、次に対数の定義により .

この対数のプロパティの使用例を次に示します。 .

次に進みましょう べき乗の対数の性質。 次数の対数は、指数と、この次数の底の係数の対数の積に等しくなります。 このべき乗の対数の性質を式として書いてみましょう。 log a b p =p・log a |b|ここで、a>0、a≠1、b および p は、次数 b p が意味を持ち、b p >0 となるような数値です。

まず、この性質を正の b について証明します。 基本的な対数恒等式により、数値 b を a log a b として表すことができ、 b p =(a log a b) p となり、べき乗の性質により、結果の式は a p・log a b に等しくなります。 したがって、等式 b p =a p・log a b が得られ、そこから対数の定義により、log a b p =p・log a b と結論付けられます。

負の b についてこの性質を証明することはまだ残っています。 ここで、負の b に対する式 log a b p は、偶数の指数 p の場合にのみ意味があることに注意してください (次数 b p の値はゼロより大きくなければならず、そうでない場合は対数が意味を成さないからです)。この場合、 b p =|b| となります。 p. 次に、 b p =|b| p =(a log a |b|) p =a p・log a |b| , ここから、log a b p =p・log a |b| 。

例えば、 ln(-3) 4 =4・ln|-3|=4・ln3 。

前のプロパティから引き継がれます 根からの対数の性質: n 乗根の対数は、分数 1/n と根号表現の対数の積に等しい。つまり、a>0、a≠1、n は 1 より大きい自然数、b>0 。

証明は、任意の正の b に対して有効な等式 (小数指数を含む指数の定義を参照) と指数の対数の特性に基づいています。 .

このプロパティの使用例を次に示します。 .

さあ証明しましょう 新しい対数底に移動するための公式親切 。 これを行うには、等式 log c b=log a b・log c a の妥当性を証明するだけで十分です。 基本的な対数恒等式により、数値 b を a log a b として表すことができ、log c b=log c a log a b となります。 次の次数の対数の特性を使用することは残ります: log c a log a b =log a b・log c a 。 これにより、等価性 log c b=log a b・log c a が証明されます。これは、対数の新しい底への移行公式も証明されることを意味します。 .

この対数の特性を使用する例をいくつか示します。 .

新しい底に移動する公式を使用すると、「便利な」底を持つ対数の処理に進むことができます。 たとえば、自然対数または 10 進対数に変更して、対数の表から対数の値を計算するために使用できます。 新しい対数の底に移動するための式を使用すると、場合によっては、他の底を持ついくつかの対数の値がわかっている場合に、特定の対数の値を見つけることもできます。

c=b の形式の新しい対数底への移行式の特殊なケースがよく使用されます。 これは、log a b と log b a が互いに逆数であることを示しています。 例えば、 .

対数の値を求めるのにも便利な公式もよく使われます。 私たちの言葉を確認するために、これを使用して の形式の対数値を計算する方法を示します。 我々は持っています 。 式を証明するには、対数 a の新しい底に移動する式を使用するだけで十分です。 .

対数の比較の性質を証明することはまだ残っています。

逆の方法を使ってみましょう。 a 1 >1、a 2 >1、および a 1 2、および 0 1 について、log a 1 b≤log a 2 b が真であると仮定します。 対数の性質に基づいて、これらの不等式は次のように書き直すことができます。 そして これらから、それぞれ、log b a 1 ≤ log b a 2 および log b a 1 ≧log b a 2 が得られます。 次に、べき乗の性質により、 同じ根拠で等式 b log b a 1 ≧ b log b a 2 および b log b a 1 ≧ b log b a 2 が満たされなければなりません。つまり、 a 1 ≧ a 2 です。 したがって、条件 a 1 2 に矛盾することがわかりました。 これで証明は完了です。

対数の基本的な性質

• レッスン用の教材
• すべての数式をダウンロードする

対数は、他の数値と同様、あらゆる方法で加算、減算、変換できます。 しかし、対数はまったく普通の数ではないため、ここには次のような規則があります。 主な特性.

これらのルールを必ず知っておく必要があります。これらのルールがなければ、深刻な問題は何一つ解決できません。 対数問題。 さらに、それらの数は非常に少なく、1日ですべてを学ぶことができます。 それでは始めましょう。

対数の加算と減算

同じ底を持つ 2 つの対数、log a x と log a y を考えてみましょう。 その後、それらを加算および減算し、次の操作を行うことができます。

したがって、対数の合計は積の対数に等しく、差は商の対数に等しくなります。 注記： 重要な瞬間ここ - 同一の根拠。 理由が異なる場合、これらのルールは機能しません。

これらの公式は計算に役立ちます 対数表現個々の部分が数えられない場合でも (「対数とは」のレッスンを参照)。 例を見て、次のことを確認してください。

タスク。 式の値を見つけます: log 6 4 + log 6 9。

対数の底は同じなので、合計の公式を使用します。
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2。

タスク。 式の値を見つけます: log 2 48 − log 2 3。

ベースは同じなので、差分の式を使用します。
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4。

タスク。 式の値を見つけます: log 3 135 − log 3 5。

ここでもベースは同じなので、次のようになります。
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3。

ご覧のとおり、元の式は「悪い」対数で構成されており、個別に計算されていません。 しかし、変換後は完全に正規の数値が得られます。 多くはこの事実に基づいて構築されています 試験用紙。 はい、統一国家試験では、テストのような表現が真剣に (場合によってはほとんど変更なしで) 提供されます。

対数から指数を抽出する

では、タスクを少し複雑にしてみましょう。 対数の底または引数が累乗の場合はどうなるでしょうか? 次に、次の規則に従って、対数の符号からこの次数の指数を取り出すことができます。

• log a x n = n · log a x ;
• 
• 

それに気づくのは簡単です 最後のルール最初の 2 つに続きます。 ただし、とにかく覚えておいたほうがよいでしょう。場合によっては、計算量が大幅に削減されます。

もちろん、対数の ODZ (a > 0、a ≠ 1、x > 0) が観察されていれば、これらすべてのルールは意味を持ちます。そしてもう 1 つ、すべての式を左から右へだけでなく、その逆にも適用することを学びましょう。 、つまり 対数記号の前の数値を対数そのものに入力できます。 これが最も頻繁に必要となるものです。

タスク。 式の値を見つけます: log 7 49 6 。

最初の式を使用して、引数内の次数を取り除きましょう。
対数 7 49 6 = 6 対数 7 49 = 6 2 = 12

タスク。 式の意味を調べます。

[写真のキャプション]

分母には​​対数が含まれており、その底と引数は正確な累乗であることに注意してください: 16 = 2 4 ; 49 = 7 2. 我々は持っています：

[写真のキャプション]

最後の例については、もう少し説明が必要だと思います。 対数はどこへ行ったのでしょうか? 最後の瞬間まで、私たちは分母だけを扱います。 そこに立っている対数の底と引数をべき乗の形で提示し、指数を取り除きました。「3 階建て」の分数が得られました。

次に、主要部分を見てみましょう。 分子と分母には同じ数値が含まれます: log 2 7。log 2 7 ≠ 0 なので、分数を減らすことができます。分母には 2/4 が残ります。 算術の規則によれば、4 を分子に移すことができ、それが行われたのです。 結果は、答えは「２」でした。

新しい基盤への移行

対数の加算と減算のルールについて、これらは同じ底を使用した場合にのみ機能することを特に強調しました。 理由が違っていたらどうなるでしょうか？ それらが同じ数の正確なべき乗ではない場合はどうなるでしょうか?

新しい財団への移行のための公式が役に立ちます。 それらを定理の形で定式化してみましょう。

対数 log a x を与えます。 次に、c > 0 および c ≠ 1 であるような任意の数値 c について、等式が真になります。

[写真のキャプション]

特に、c = x と設定すると、次のようになります。

[写真のキャプション]

2 番目の式から、対数の底と引数を交換できることがわかりますが、この場合、式全体が「ひっくり返る」ことになります。 対数が分母に表示されます。

これらの式は従来のものではほとんど見られません。 数値表現。 判断するだけでどれだけ便利かを評価できる 対数方程式そして不平等。

しかし、新たな基盤に移行する以外には全く解決できない問題もある。 いくつか見てみましょう:

タスク。 式の値を見つけます: log 5 16 log 2 25。

両方の対数の引数には正確な累乗が含まれることに注意してください。 指標を取り出してみましょう: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

次に、2 番目の対数を「反転」してみましょう。

[写真のキャプション]

因数を並べ替えても積は変わらないので、落ち着いて4と2を掛けてから対数を扱いました。

タスク。 式の値を見つけます: log 9 100 lg 3。

最初の対数の底と引数は正確な累乗です。 これを書き留めてインジケーターを取り除きましょう。

[写真のキャプション]

次に、新しい底に移動して 10 進対数を取り除きましょう。

[写真のキャプション]

基本対数恒等式

多くの場合、解法プロセスでは、数値を特定の底の対数として表す必要があります。 この場合、次の公式が役に立ちます。

1. n = ログ a n

2. 最初のケースでは、数値 n が引数の指数になります。 n は単なる対数値であるため、数値 n は何でも構いません。

   2 番目の式は実際には定義を言い換えたものです。 それが「基本対数恒等式」と呼ばれるものです。

   実際、数値 b を、数値 b の累乗が数値 a になるように累乗するとどうなるでしょうか? そうです。結果は同じ数値 a です。 この段落をもう一度注意深く読んでください。多くの人がここで行き詰まってしまいます。

   新しい底に移動するための公式と同様に、基本的な対数恒等式が唯一可能な解決策である場合があります。

   [写真のキャプション]

   log 25 64 = log 5 8 - 対数の底と引数から 2 乗しただけであることに注意してください。 同じ基数でべき乗を乗算するルールを考慮すると、次のようになります。

   [写真のキャプション]

   知らない人もいるかもしれませんが、これは統一国家試験の実際の課題でした :)

   対数単位と対数ゼロ

   結論として、プロパティとは言い難い 2 つの恒等式を示します。むしろ、それらは対数の定義の結果です。 それらは常に問題に登場し、驚くべきことに「上級」の生徒でも問題を引き起こします。

   1. log a a = 1 は対数単位です。 必ず覚えておいてください。底 a の底に対する対数自体は 1 に等しいということです。
   2. log a 1 = 0 は対数ゼロです。 基数 a は何でも構いませんが、引数に 1 が含まれている場合、対数は 0 に等しくなります。 0 = 1 は定義の直接的な結果であるためです。

   それがすべてのプロパティです。 ぜひ実践してみてください！ レッスンの初めにカンニングペーパーをダウンロードして印刷し、問題を解いてください。

   対数。 対数のプロパティ (加算と減算)。

   対数の性質その定義に従います。 そしてその数の対数は bに基づく あ数値を累乗する必要がある指数として定義されます ある番号を取得する b(対数は正の数に対してのみ存在します)。

   この公式から、計算は次のようになります。 x=log a b、方程式を解くのと同じです a x =b。例えば、 対数 2 8 = 3なぜなら 8 = 2 3 。 対数を定式化すると、次のことを正当化できます。 b=a c、次に数値の対数 bに基づく ある等しい と。 対数の話題がべき乗の話題と密接に関係していることも明らかです。

   他の数値と同様に、対数でも次のことができます。 加算、減算の演算そしてあらゆる方法で変身します。 しかし、対数は完全に普通の数ではないという事実により、ここでは独自の特別な規則が適用されます。 主な特性.

   対数の加算と減算。

   同じ底を持つ 2 つの対数を考えてみましょう。 ×を記録するそして ログを記録する。 これにより、加算および減算演算を実行できるようになります。

   ご覧のとおり、 対数の和積の対数に等しい、そして 違い 対数- 商の対数。 さらに、これは数字の場合にも当てはまります。 あ、 バツそして でポジティブで a≠1。

   これらの式の主な側面は同じ塩基であることに注意することが重要です。 根拠が異なる場合、このルールは適用されません。

   同じ底を持つ対数の加算と減算のルールは、左から右へだけでなく、その逆にも読み取られます。 その結果、積の対数と商の対数に関する定理が得られます。

   積の対数 2 つの正の数 合計に等しいそれらの対数 ; この定理を言い換えると、次の数値が得られます。 あ, バツそして でポジティブで a ≠ 1、 それ：

   商の対数 2 つの正の数は、被除数と除数の対数の差に等しくなります。 別の言い方をすれば、数字であれば、 あ, バツそして でポジティブで a ≠ 1、 それ：

   上記の定理を適用して解いてみましょう 例:

   もし数字が バツそして で負の場合 積対数の公式意味がなくなってしまいます。 したがって、次のような書き込みは禁止されています。

   log 2 (-8) と log 2 (-4) という式がまったく定義されていないため (対数関数) で= ログ 2 バツ正の引数値に対してのみ定義されています バツ).

   積の定理 2 つの要素だけでなく、無制限の数の要素にも適用できます。 これは、あらゆる自然に対して、 kおよび任意の正の数 バツ 1 , バツ 2 , . . . ,×nアイデンティティがあります:

   から 対数商の定理対数のもう 1 つの特性を取得できます。 ログを記録することは常識です ある 1= 0、したがって

   これは、次の等式が成り立つことを意味します。

   2 つの逆数の対数同じ理由で、符号のみが互いに異なります。 それで：

   対数。 対数の性質

   対数。 対数の性質

   平等について考えてみましょう。 と の値を教えてください。 の値を見つけたいと考えています。

   つまり、 を取得するためにコックする必要がある指数を探しています。

   させて 変数は任意の実数値を取ることができ、変数には次の制限が課されます: o" title="a>o"/> 、1″ title=»a1″/>、0″ title=»b>0″ />

   と の値がわかっていて、未知のものを見つけるという課題に直面した場合、この目的のために、と呼ばれる数学的演算が導入されます。 対数.

   私たちが取る価値を見つけるには 数値の対数による 基礎 :

   数値の底に対する対数は、 を得るために累乗する必要がある指数です。

   あれは 基本対数恒等式:

   o» title=»a>o»/> 、1″ title=»a1″/>、0″ title=»b>0″/>

   本質的には数学的な表記法です 対数の定義.

   対数の数学的演算は、べき乗の演算の逆です。 対数の性質は次数の性質と密接に関係しています。

   主なものを挙げてみましょう 対数の性質:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   次のプロパティ グループを使用すると、式の指数を対数の符号の下に表すか、対数の符号の前にある係数の形式で対数の底に立って表すことができます。

   6.

   7.

   8.

   9.

   次の数式グループを使用すると、特定の底をもつ対数から任意の底をもつ対数に移動できます。 新しい拠点への移行方程式:

   10.

   12. (特性 11 からの帰結)

   

   次の 3 つのプロパティはあまり知られていませんが、対数方程式を解くときや、対数を含む式を簡略化するときによく使用されます。

   13.

   14.

   15.

   特殊なケース：

   — 10 進対数

   — 自然対数

   対数を含む式を簡略化する場合、次の一般的なアプローチが使用されます。

   1. 紹介 小数普通のものの形で。

   2. 帯分数仮分数で表します。

   3. 対数の底と対数の符号の下にある数値を単純な因数に分解します。

   4. すべての対数を同じ底に換算しようとします。

   5. 対数の特性を適用します。

   対数を含む式を簡略化する例を見てみましょう。

   例1.

   計算します:

   すべての指数を単純化してみましょう。私たちの仕事は、指数の底と同じ数値を底とする対数に換算することです。

   ==(プロパティ 7 による)=(プロパティ 6 による) =

   取得したインジケーターを元の式に置き換えてみましょう。 我々が得る：

   答え: 5.25

   例 2. 計算します。

   

   すべての対数を底 6 に換算してみます (この場合、分数の分母の対数が分子に「移行」します)。

   対数記号の下の数値を単純な因数に分解してみましょう。

   プロパティ 4 と 6 を適用してみましょう。

   代替品を紹介しましょう

   我々が得る：

   答え: 1

   対数 . 基本的な対数恒等式。

   対数の性質。 10 進対数。 自然対数。

   対数 N を基数とする正の数 (b > 0, b 1) N を得るために b を累乗する必要がある指数 x です .

   このエントリは次と同等です。 b x = N .

   例: 3 4 = 81 なので、log 3 81 = 4。

   対数 1/3 27 = – 3、(1/3) - 3 = 3 3 = 27 より。

   上記の対数の定義は恒等式として書くことができます。

   

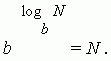
   対数の基本的な性質。

   2) log 1 = 0、つまり b 0 = 1 .

   3) 積の対数は、因子の対数の合計に等しくなります。

   4) 商の対数は、被除数と除数の対数の差に等しくなります。

   5) べき乗の対数は、指数とその底の対数の積に等しくなります。

   このプロパティの結果は次のようになります。 根の対数 根号の対数を根のべき乗で割ったものに等しい：

   

   6) 対数の底が度の場合、値は インジケーターの逆数度は、対数韻記号から取り出すことができます。

   

   最後の 2 つのプロパティは 1 つに結合できます。

   

   7) 遷移係数の式 (つまり、ある対数の底から別の底への遷移):

   

   特別な場合には、 N=a我々は持っています：

   

   10 進対数 呼ばれた 底対数 10. それは lg で表されます。 ログ10 N= ログ N。 数値 10、100、1000、... の対数。 p はそれぞれ 1、2、3、…、つまり ポジティブなものがたくさんある

   単位、対数の 1 の後にゼロが何個あるか。 数値の対数 0.1、0.01、0.001、... p はそれぞれ -1、-2、-3、…、つまり 1 の前の対数のゼロと同数の負の 1 を持ちます (ゼロの整数を含む)。 他の数値の対数には、と呼ばれる小数部分があります。 仮数。 対数の整数部分を次のように呼びます。 特性。 実際に使用するには、10 進対数が最も便利です。

   自然対数 呼ばれた 底対数 e。 それは ln で表されます。 ログ e N= ログ N。 番号 eは無理数であり、その近似値は 2.718281828 です。 それは、数値が傾向にある極限です (1 + 1 / n) n無制限に増加 n（cm。 最初の素晴らしい制限「番号シーケンスの制限」ペー​​ジを参照)。
   奇妙に思われるかもしれませんが、 自然対数関数解析に関するさまざまな操作を行う際に非常に便利です。 底に対する対数の計算 e他の理由よりもはるかに速く実行されます。

• 今日、ロシアで養子を迎えるには何が必要でしょうか? ロシアにおける養子縁組には、責任ある個人の決定に加えて、候補者を国家が確認するための多くの手続きが含まれる。 準備段階での厳格な選択は、より多くの […]
• ロシア全土の税務台帳からの TIN または OGRN に関する無料情報 - オンライン 統一税務サービス ポータルで、以下の情報を入手できます。 州登録 法人, 個人起業家, […]
• 書類なしで運転した場合の罰則（運転免許証、保険、STS） 物忘れなどにより無免許で運転し、書類なしで運転した場合に罰金を科される場合があります。 車愛好家には次のことが求められることを思い出していただきたいと思います […]
• 男性のための花。 男性にどんな花を贈れますか？ 男性にどんな花を贈れますか？ 「雄花」はあまりありませんが、男性に贈られる花もあります。 あなたの目の前にある小さな花リスト: 菊。 バラ。 カーネーション。 […]
• 内部メモは、企業の内部環境で使用され、現在の生産上の問題を迅速に解決するために使用される特別な形式の文書です。 通常、このドキュメントは、いくつかの内容を紹介する目的で作成されます […]
• 年金積立部分をズベルバンクからいつ、どのように受け取るのですか? ズベルバンクは国民年金基金のパートナー銀行です。 これに基づき、積立年金に登録した国民は積立部分を移管することができる […]
• ウリヤノフスク州の児童手当と ウリヤノフスク地方 2018年 さらに、すべての被験者は連邦法によって承認されたプログラムを実施しています。 誰がどのようなメリットを期待できるかを見てみましょう。 地方自治体はどのように […]
• 詳細ガイド利益を代表する委任状を作成する方法 個人法廷で 民事訴訟または仲裁訴訟、行政訴訟または刑事訴訟において、原告と被告の両方の利益を弁護士が代理することができます。 […]

自然対数、グラフ、定義域、一連の値、基本公式、導関数、積分、べき級数展開、および複素数を使用した関数 ln x の表現の基本的な特性が示されています。

意味

自然対数関数 y = lnx、の逆 指数関数的, x = e y 、そして は 対数数値 e に基づいて: ln x = log e x.

自然対数は、その導関数が最も単純な形式であるため、数学で広く使用されています。 (ln x)' = 1/ x.

ベース 定義、自然対数の底は次の数です。 e:
e ≅ 2.718281828459045...;
.

関数 y = のグラフ lnx.

自然対数のグラフ (関数 y = lnx) から得られます 指数関数的なグラフィックス直線 y = x に対する鏡面反射。

自然対数は次のように定義されます。 正の値変数x。 それはその定義領域内で単調増加します。

×時 → 0 自然対数の極限はマイナス無限大 (-∞) です。

x → + ∞ なので、自然対数の極限はプラス無限大 (+ ∞) です。 x が大きい場合、対数は非常にゆっくりと増加します。 どれでも べき乗関数正の指数 a を持つ x a は、対数よりも速く増加します。

自然対数の性質

定義範囲、値のセット、極値、増加、減少

自然対数は単調増加関数であるため、極値はありません。 自然対数の主な特性を表に示します。

ln x 値

ln1 = 0

自然対数の基本公式

逆関数の定義から次の式が得られます。

対数の主な性質とその結果

塩基置換式

任意の対数は、塩基置換式を使用して自然対数で表現できます。

これらの公式の証明はセクションで示されています "対数".

逆関数

自然対数の逆数は次のようになります。 指数.

の場合、

もしそうなら。

導関数 ln x

自然対数の微分:
.
係数 x の自然対数の微分:
.
n次微分:
.
数式の導出 > > >

積分

積分が計算されます 部品ごとの統合 :
.
それで、

複素数を使った式

複素変数 z の関数を考えてみましょう。
.
複素変数を表現してみよう zモジュール経由 rそして議論 φ :
.
対数の特性を使用すると、次のようになります。
.
または
.
引数 φ は一意に定義されません。 置いたら
ここで、n は整数です。
n が異なっても同じ番号になります。

したがって、複素変数の関数としての自然対数は、単一値の関数ではありません。

べき級数展開

拡張が行われると、次のようになります。

参考文献:
で。 ブロンスタイン、K.A. Semendyaev、エンジニアと大学生のための数学ハンドブック、「Lan」、2009 年。

数値の対数 N に基づく あ 指数と呼ばれる バツ 、そこにビルドする必要があります あ 番号を取得する N

ただし、
,
,

対数の定義から次のことがわかります。
、つまり
- この等式は、基本的な対数恒等式です。

10 を底とする対数は 10 進対数と呼ばれます。 の代わりに
書く
.

底の対数 e ナチュラルと呼ばれ、指定されています
.

対数の基本的な性質。

1 の対数は、どの底でも 0 に等しくなります。

積の対数は、因子の対数の合計に等しくなります。

3) 商の対数は対数の差に等しい

要素
対数から底への遷移係数と呼ばれます ある 底の対数に b .

プロパティ 2 ～ 5 を使用すると、多くの場合、複雑な式の対数を、対数に対する単純な算術演算の結果に換算することができます。

例えば、

このような対数の変換を対数と呼びます。 対数の逆変換は増強と呼ばれます。

第 2 章 高等数学の要素。

1. 限界

機能の限界
が有限数 A である場合、 xx 0 あらかじめ決められたそれぞれに対して
、そのような数字があります
それはすぐに
、 それ
.

制限のある関数は、制限された関数とは微小な差があります。
、ここで、- b.m.v.、つまり
.

例。 機能を考えてみる
.

努力するとき
、 関数 y ゼロになる傾向があります:

1.1. 限界に関する基本定理。

定数値の制限はこの定数値に等しい

.

有限数の関数の和（差）の極限は、これらの関数の極限の和（差）に等しい。

有限数の関数の積の極限は、これらの関数の極限の積に等しい。

分母の限界がゼロでない場合、2 つの関数の商の限界は、これらの関数の限界の商と等しくなります。

素晴らしい限界

,
、 どこ

1.2. 制限値の計算例

ただし、すべての制限がそれほど簡単に計算できるわけではありません。 多くの場合、制限を計算すると、次のような種類の不確実性が明らかになります。 または 。

.

2. 関数の導関数

関数を持たせましょう
、セグメント上で連続
.

口論 いくらか増加しました
。 その後、関数はインクリメントを受け取ります
.

引数の値 関数値に対応します
.

引数の値
関数値に対応します。

したがって、 。

この比率の限界を次のように求めてみましょう。
。 この制限が存在する場合、それは指定された関数の導関数と呼ばれます。

定義 3 指定された関数の導関数
引数による 引数の増分が任意にゼロになる傾向がある場合、関数の増分と引数の増分との比率の限界と呼ばれます。

関数の導関数
次のように指定できます。

; ; ; .

定義 4 関数の導関数を求める操作は、と呼ばれます。 差別化。

2.1. 導関数の機械的な意味。

ある剛体または物質点の直線運動を考えてみましょう。

いつかの時点でさせてください 移動点
遠くにいた 開始位置から
.

一定の時間が経過した後
彼女は遠くへ引っ越した
。 態度 =- 平均速度質点
。 次のことを考慮して、この比率の限界を見つけてみましょう。
.

したがって、質点の瞬間的な移動速度の決定は、時間に対する経路の導関数を求めることに帰着します。

2.2. 幾何学的な意味派生関数

グラフィカルに関数を定義してみましょう
.

米。 1. 導関数の幾何学的意味

もし
、次にポイントします
、カーブに沿って移動し、ポイントに近づきます
.

したがって、
、つまり 引数の指定された値に対する導関数の値 指定された点における軸の正の方向との接線によって形成される角度の正接に数値的に等しい
.

2.3. 基本的な微分公式の表。

べき乗関数

指数関数

対数関数

三角関数

逆三角関数

2.4. 微分の法則。

の派生語

関数の和（差）の導関数

2 つの関数の積の導関数

2 つの関数の商の導関数

2.5. の派生語 複素関数.

関数を与えてみよう
という形で表現できるように、

そして
、ここで変数は が中間引数である場合、

複素関数の導関数は、中間引数に関する指定された関数の導関数と、x に関する中間引数の導関数の積に等しくなります。

例1.

例2。

3. 微分機能。

そこにおいて
、ある区間で微分可能
放っておいて で この関数には導関数があります

,

そうすれば書けます

(1),

どこ - 無限微量、

いつから

等式のすべての項 (1) を乗算します。
我々は持っています：

どこ
- b.m.v. 高次。

マグニチュード
関数の微分と呼ばれる
そして指定されている

.

3.1. 差分の幾何学的値。

関数を与えてみよう
.

図2. 差動の幾何学的意味。

.

明らかに、関数の微分は、
は、特定の点における接線の縦座標の増分に等しくなります。

3.2. さまざまな次数の微分と微分。

もしそこにあるなら
、 それから
を一次導関数といいます。

一次導関数の導関数は二次導関数と呼ばれ、次のように書かれます。
.

関数の n 次導関数
は (n-1) 次導関数と呼ばれ、次のように書かれます。

.

関数の微分の微分を2次微分または2階微分といいます。

.

.

3.3 微分を使用した生物学的問題の解決。

タスク1。 研究により、微生物のコロニーの成長は法則に従っていることが示されています。
、 どこ N – 微生物の数（千単位）、 t – 時間 (日)。

b) この期間中にコロニーの人口は増加しますか、それとも減少しますか?

答え。 コロニーのサイズは大きくなります。

タスク 2. 湖の水は定期的に検査され、病原性細菌の含有量が監視されます。 を通して t 検査から数日後の細菌濃度は比率によって決定されます。

.

湖の細菌濃度が最小値になるのはいつですか。また、湖で泳ぐことができるようになりますか?

解決策: 関数は、導関数がゼロのときに最大値または最小値に達します。

,

最大値または最小値が 6 日以内になるようにしましょう。 これを行うために、二次導関数を取得しましょう。

回答: 6 日後には細菌の濃度は最小になります。